Предмет: Математика,
автор: aleksmishkova
Найти предел ( не пользуясь правилом ЛОПИТАЛЯ)
Приложения:
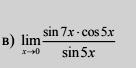
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Uticall
Предмет: Русский язык,
автор: Fima11
Предмет: Українська мова,
автор: natasik386
Предмет: Биология,
автор: юлия5хозяенко
Предмет: Математика,
автор: tirpu85