Запиши ответ Прямая проходит через точку А(-1; — 5) 4 и касается гиперболы у При каком — T значении хэта прямая пересекает ось абсцисс? Ответ:
Ответы
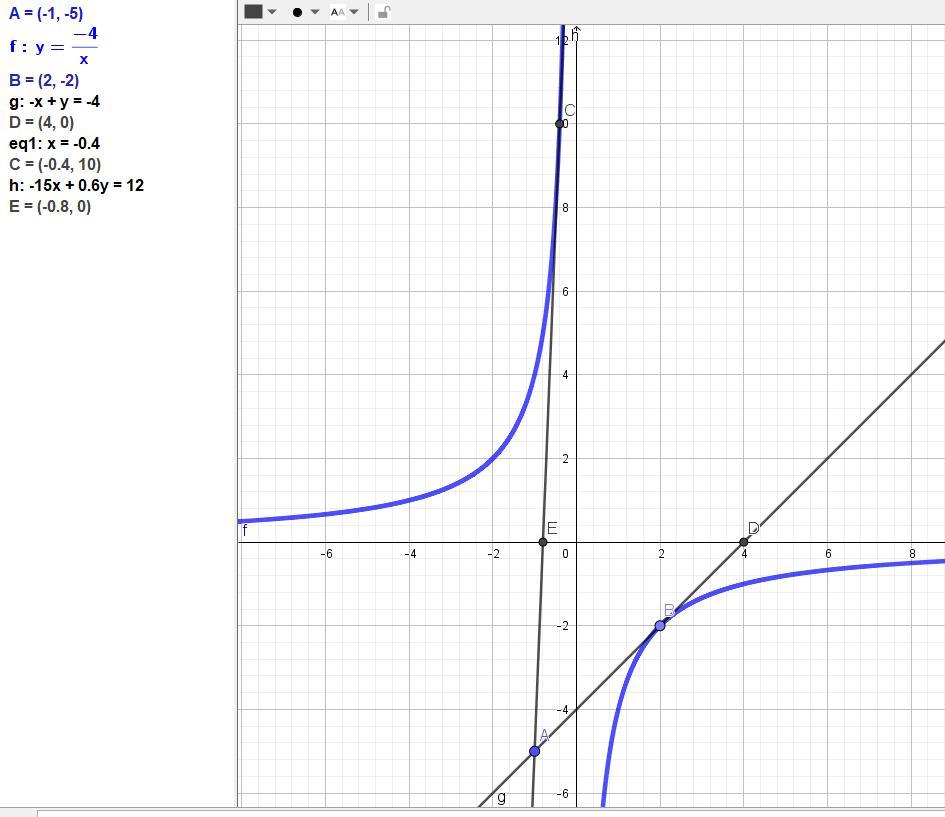
Задача. Прямая проходит через точку А(-1; -5) и касается гиперболы у= -4/х.
При каком значении х эта прямая пересекает ось абсцисс?
Составляем уравнение касательной, примем координаты точки касания (a; b)
Находим f(a)= -4/a.
Уравнение касательной у=y’(х-х0)+y(х0).
Находим производную функции у= -4/х: y’ = -4*(-1/x²) = 4/x².
Теперь подставим в уравнение производной координаты точки касания.
Уравнение касательной у= (4/a²) (х-a) + (-4/a).
Так как касательная проходит через точку А(-1;-5), то ее координаты удовлетворяют уравнению касательной.
-5 = (4/a²)(-1 – a) – (4/a),
-5 = ((-4 – 4a)/a²) – (4/a), приведём к общему знаменателю.
-5a² = -4 – 4a – 4a,
5a²– 8a – 4 = 0, получили квадратное уравнение.
Ищем дискриминант:
D=(-8)^2-4*5*(-4)=64-4*5*(-4)=64-20*(-4)=64-(-20*4)=64-(-80)=64+80=144;
Дискриминант больше 0, уравнение имеет 2 корня:
a_1=(√144-(-8))/(2*5)=(12-(-8))/(2*5)=(12+8)/(2*5)=20/(2*5)=20/10=2;
a_2=(-√144-(-8))/(2*5)=(-12-(-8))/(2*5)=(-12+8)/(2*5)=-4/(2*5)=-4/10=-0.4.
Составим уравнение касательной для каждого значения а.
При а=2 имеем у(2)= (4/2²) (х-2) + (-4/2) = (х-2) – 2 = х-4.
При а=0,4 имеем у(0,4)= (4/0,4²) (х-(-0,4)) + (-4/-0,4) = 25(х+0,4) + 10 = 25х+20.
Для определения точек пересечения касательных с осью Ох подставим значение у = 0.
0 = х-4, отсюда х = 4.
0 = 25х+20, отсюда х = -20/25 = -0,8.
Ответ: х = 4, х = -0,8.