Предмет: Алгебра,
автор: frogg0
найти площадь фигуры ограниченной линиями + чертеж
Приложения:
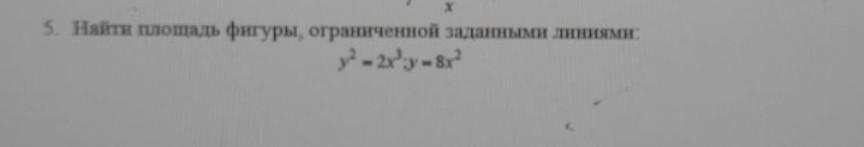
Ответы
Автор ответа:
1
Объяснение:
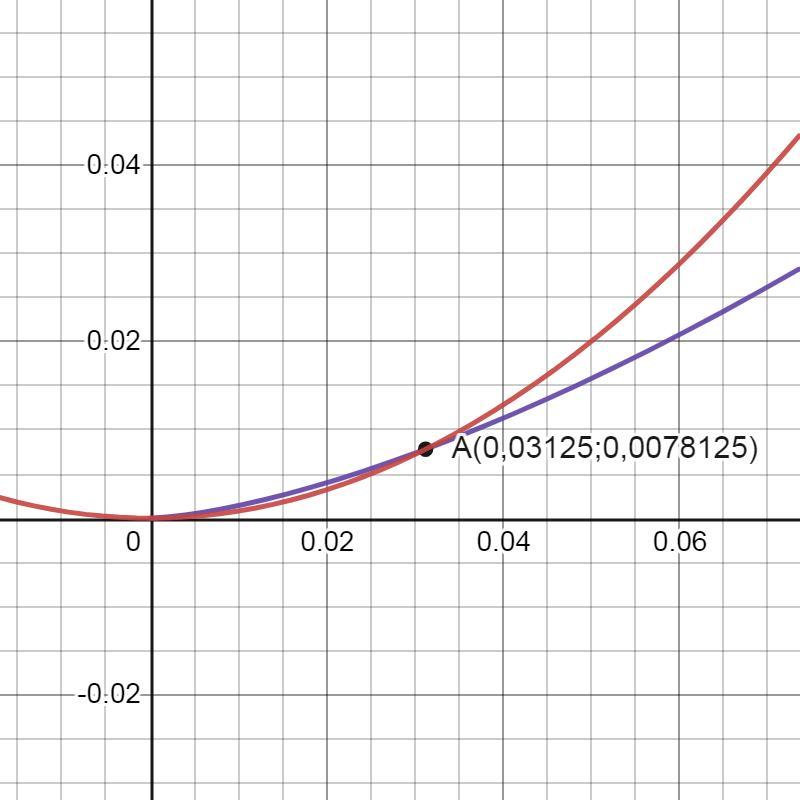
Ответ: S≈0,000016276 кв. ед.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Школаад111
Предмет: Русский язык,
автор: al2405
Предмет: Русский язык,
автор: лалалоалс
Предмет: Английский язык,
автор: Koмаr200120
Предмет: Геометрия,
автор: Infalible