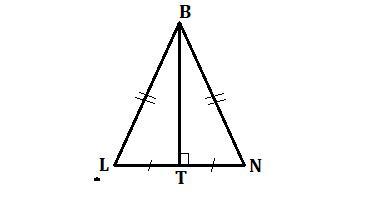
6. BT - медиана равнобедренного треугольника LBN. LN - основание . Периметр треугольника LBN равен 50 м, а периметр треугольника LBT -40 м. Найдите длину медианы ВТ. Начерти чертеж к задаче.
Ответы
Ответ:
15 м
Пошаговое объяснение:
I способ.
Составим систему уравнений.
P ΔLBN = LB + BN + LN
LB = BN, по свойству равнобедренного треугольника.
Пусть x м - LB и BN, тогда y м - LN
x + x + y = 50 - 1 уравнение
Составляем 2 уравнение:
P ΔLBT = LB + BT + LT
x м - LB
BT - высота, медиана, биссектриса (по свойству равнобедренного треугольника), значит LT = TN = 1/2LN
Тогда 1/2y м - LT
ΔLBT - прямоугольный, так как BT - высота
⇒ по теореме Пифагора:
м - BT
- 2 уравнение
Решим получившуюся систему уравнений:
В числителе 2 дроби видим формулу сокращённого умножения - квадрат разности. Раскладываем по формуле: (a - b)² = a² - 2ab + b²
17 м - LB
17 + 17 + y = 50
y = 50 - 17 - 17
y = 50 - 34
y = 16
16 м - LN
LT = 1/2LN = 16/2 = 8 м
м
II способ.
P ΔLBN = LB + LN + BN
Так как ΔLBN - равнобедренный ⇒ LB = BN (по свойству равнобедренного треугольника)
⇒ P ΔLBN = 2LB + LN
2LB + LN = 50 м
P ΔLBT = LB + BT + LT
Так как BT - медиана, по условию ⇒ LT = 1/2LN
⇒ P ΔLBT = LB + BT + 1/2LN
LB + BT + 1/2LN = 40 м | · 2
2LB + 2BT + LN = 80 м
Так как 2LB + LN = 50 м ⇒ 2BT = 80 - 50 = 30 м
⇒ BT = 30 : 2 = 15 м