Question

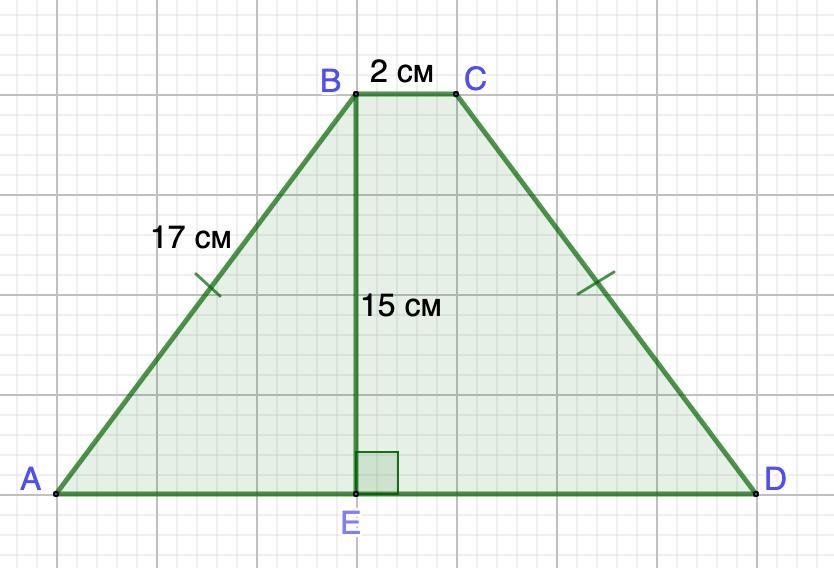
в равнобедренной трапеции боковая сторона 17 см меньшее основание 2 см а высота равна 15 см найдите площадь трапеции​

Answer 1

Ответ:

150 см²

Пошаговое объяснение:

Дано: ABCD - равнобедренная трапеция.

АВ = 17 см; ВС = 15 см; ВЕ = 15 см - высота.

Найти: S трапеции.

Решение:

Площадь трапеции найдем по формуле:

$\displaystyle S=\frac{a+b}{2}*h$ ,

где a и b - основания трапеции, h - высота.

Необходимо найти большее расстояние:

Рассмотрим ΔАВЕ - прямоугольный.

По теореме Пифагора найдем АЕ:

$\displaystyle AE=\sqrt{AB^2-BE^2}=\sqrt{289-225}=\sqrt{64}=8\;_{(CM)}$

• В равнобедренной трапеции высота, опущенная из вершины тупого угла, делит большее основание на части, меньшая из которых равна полуразности оснований.

⇒

$\displaystyle AE=\frac{AD-BC}{2}\\\\8=\frac{AD-2}{2}\\\\AD-2=16\\\\AD=18\;_{(CM)}$

теперь можем найти S:

$\displaystyle S=\frac{BC+AD}{2}*BE\\\\S=\frac{2+18}{2}*15=150\;_{(CM^2)}$