Question

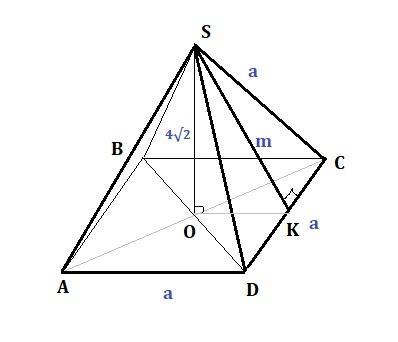
Найдите площадь поверхности правильной четырехугольной пирамиды, у которой боковые грани – правильные треугольники, а высота пирамиды равна 4√2 с. см.​

Answer 1

Объяснение:

Дано: SABCD - правильная четырехугольная пирамида.

Боковые грани – правильные треугольники.

ABCD - квадрат.

SO = 4√2 см.

Найти: S полн.

Решение:

По условию все ребра пирамиды равны.

1. Рассмотрим ΔACD - прямоугольный.

Пусть AD = DC = а

По теореме Пифагора:

$\displaystyle AC^2=AD^2+DC^2=a^2+a^2=2a^2\\\\AC=a\sqrt{2}\;_{(CM)}$

• Диагонали квадрата точкой пересечения делятся пополам.

⇒ $\displaystyle AO=\frac{a\sqrt{2} }{2} \;_{CM)}$

2. Рассмотрим ΔAOS - прямоугольный.

По теореме Пифагора:

$\displaystyle AS^2=AO^2+SO^2\\\\a^2=\frac{a^2*2}{4}+4^2*2\\\\a^2-\frac{a^2}{2}=32\\\\\frac{a^2}{2}=32\\\\a^2=64\\a=8\;_{(CM)}$

3. S полн. = S осн. +S бок.

S бок. равна площади четырех равносторонних треугольников.

Площадь равностороннего треугольника найдем по формуле:

$\displaystyle S\Delta=\frac{a^2\sqrt{3} }{4} \\\\S\Delta=\frac{64\sqrt{3} }{2}=32\sqrt{3}\;_{(CM^2)}$

⇒ S бок. = 32√3 * 4 = 128√3 (см²)

Площадь основания:

$\displaystyle S_{OCH}=a^2\\S_{OCH}=64\;_{CM^2}$

Площадь полной поверхности:

S полн. = (128√3 + 64) см²

Answer 2

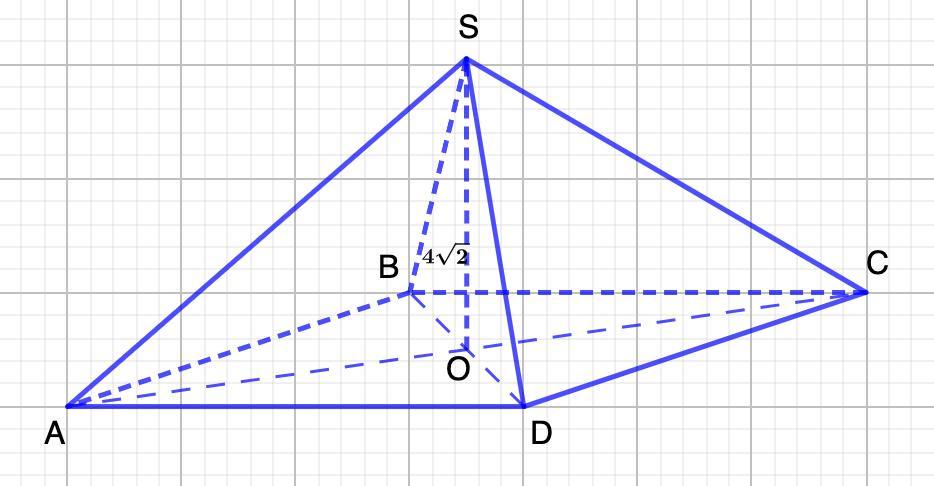
Ответ:

Sпол = 64(1+√3) см²

Объяснение:

• Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.

Sполн. = Sбок. + Sосн.

Так как основанием правильной четырёхугольной пирамиды является квадрат, то площадь основания вычисляется по формуле:

Sосн = а², а - сторона квадрата

Формула площади боковой поверхности правильной пирамиды (Sбок):

Sбок = $\dfrac{1}{2} *P*m$,

где Р - периметр основания, Р=4а, m-апофема (опущенный перпендикуляр SK из вершины S, на ребро основания DC)

Так как боковые грани – правильные треугольники, то высота SK является так же медианой: КС= DC/2 = а/2. Стороны SC=DC=SD=a.

∠SCD=∠SDC=∠DSC=60°.

1. Рассмотрим прямоугольный треугольник SKC.

$m=SK=SC*sin 60=\dfrac{a\sqrt{3} }{2}$

SO⊥(ABC) ⇒ SO⊥OK - как высота пирамиды, SK⊥DC - апофема, ⇒OK⊥DC (по теореме о трёх ⊥). ОК= а/2

    2. Рассмотрим прямоугольный треугольник SOK.

По теореме Пифагора:

$SO^{2} +OK^{2} =SK^{2} \\\\(4\sqrt{2} )^{2} +(\dfrac{a}{2} )^{2} =(\dfrac{a\sqrt{3} }{2} )^{2} \\\\32+\dfrac{a^{2} }{4} =\dfrac{3a^{2} }{4} \\\\\\2a^{2} =128\\\\a=\sqrt{64} \\\\a= 8$

  3. Sполн. =  а² + 2*a*m =

$= 8^{2} +2*8*\dfrac{8\sqrt{3} }{2} = 64+64\sqrt{3} =64(1+\sqrt{3} )$