Предмет: Алгебра,
автор: tokt9861
У простите выражения,пжпжпдпд
Приложения:
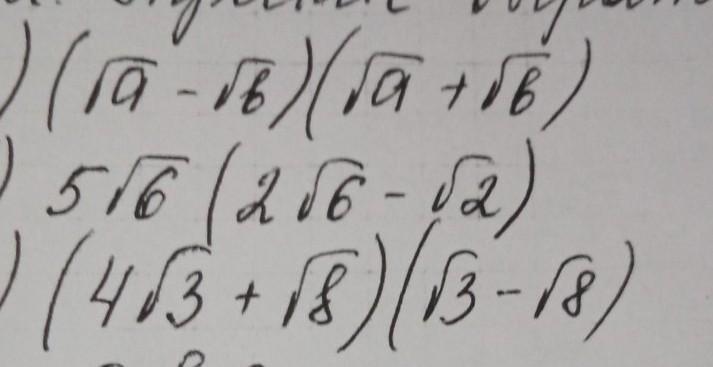
Ответы
Автор ответа:
1
Объяснение:
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: дри
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: imran2002
Предмет: Биология,
автор: bobov2003