Question

У трикутник вписано півколо, яке дотикається до двох сторін трикут-
ника і центр якого ділить третю сторону на відрізки 7,5 см і 10,5 см.
Знайдіть сторони трикутника, якщо його периметр 42 см.

Answer 1

Ответ:

Объяснение:

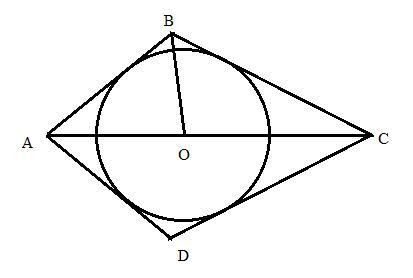
Пусть О - центр полуокружности, вписанной в △ABC. Для наглядности достроим окружность полностью, тогда она будет вписанной в четырёхугольник ABCD. Центр вписанной в любой многоугольник окружности лежит на пересечении биссектрис его углов. Значит BO - биссектриса (также как АО и ОС).

Для биссектрисы треугольника справедливо соотношение:

AO/OC=AB/BC

При этом АВ+ВС=Р-АС=42-(7,5+10,5)=24см

Решаем систему:

АВ+ВС=24

7,5/10,5=АВ/ВС

------

АВ=24-ВС

7,5/10,5=(24-ВС)/ВС

252-10,5ВС=7,5ВС

18ВС=252

ВС=252/18=14см

АВ=24-14=10см

АС=7,5+10,5=18см