ДАЮ 50 балов
Задані координати вершин піраміди M1M2M3M4 . Для всіх
варіантів виконати наступні завдання.
Завдання 2.1. Знайти кут між ребрами M1M2 та M1M4 .
Завдання 2.2. Знайти проекцію вектора M1M3 на вектор
M1M4 .
Завдання 2.3. Знайти площу грані M1M2M3 .
Завдання 2.4. Знайти довжину висоти піраміди, проведену з
вершини M4 , попередньо знайшовши об"єм піраміди.
Завдання 2.5. Встановити орієнтацію трійки векторів M1M2 ,
M1M3 і M1M4
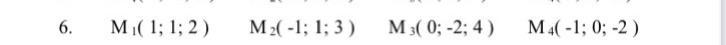
Ответы
Задані координати вершин піраміди:
M1(1; 1; 2), M2(-1; 1; 3), M3(0; -2; 4), M4(-1; 0; -2).
2.1) Знайти кут між ребрами M1M2 та M1M4.
Находим векторы и длину рёбер M1M2 и M1M4.
Длина вектора a(X;Y;Z) выражается через его координаты формулой:
a = √(X² + Y² + Z²).
Находим координаты вектора M1M2 по точкам M1( 1; 1; 2), M2 (-1; 1; 3).
M1M2 = (-1-1); 1-1; 3-2) = (-2; 0; 1).
Длина M1M2 = √((-2)² + 0² + 1²) = √(4 + 0 + 1 = √5.
Находим координаты вектора M1M4 по точкам M1( 1; 1; 2), M4(-1; 0; -2).
М1М4 = (-1-1; 0-1; -2-2) = (-2; -1; -4).
Длина M1M4 = √((-2)² + (-1)² + (-4)²) = √(4 + 1 + 16) = √21.
Угол между рёбрами М1М2 и М1М4.
cos(М1М2_М1М4) = ((-2)*(-2)+0*(-1)+1*(-4))/(√5*√21) = 0/√105 = 0.
Угол равен arccos 0 = 90 градусов.
2.2) Знайти проекцію вектора M1M3 на вектор M1M4 .
Находим координаты вектора M1M3 по точкам M1( 1; 1; 2), M3 (0; -2; 4).
Вектор M1M3 = (0-1); -2-1; 4-2) = (-1; -3; 2).
Вектор М1М4 найден и равен: М1М4 = (-2; -1; -4).
Решение в общем виде:
Пр ba = a · b
|b|
В заданном варианте: Пр(M1M3_M1M4) = M1M3*M1M4/|M1M4|.
Найдем скалярное произведение векторов M1M3*M1M4:
a · b = ax · bx + ay · by + az · bz = (-1) · (-2) + (-3) · (-1) + 2 · (-4) = 2 + 3 - 8 = -3.
Найдем модуль вектора M1M4:
|b| = √(bx² + by² + bz²) = √((-2)² + (-1)² + (-4)²) = √(4 + 1 + 16) = √21.
Пр (b)a = -3/√21 = -21/7 ≈ - 0,65465.
2.3) Знайти площу грані M1M2M3.
Площадь грани (треугольника) равна половине модуля векторного произведения векторов M1M2 = (-2; 0; 1) и M1M3 = (-1; -3; 2).
Находим их векторное произведение с применением схемы Саррюса.
I j k| I j
-2 0 1| -2 0
-1 -3 2| -1 -3 = 0i - 1j + 6k + 4j + 3i – 0k = 3i + 3j + 6k.
Векторное произведение равно (3; 3; 6). Находим площадь:
S = (1/2) √(3² + 3² + 6²) = (1/2)√(9 + 9 + 36) = (1/2)√54 = 3√6/2 ≈ 3,674.
2.4. Знайти довжину висоти піраміди, проведену з вершини M4, попередньо знайшовши об"єм піраміди.
Находим объём пирамиды, который равен (1/6) модуля смешанного произведения векторов (M1M2хM1M3)*M1M4.
Произведение (M1M2хM1M3) найдено и равно (3; 3; 6).
Вектор М1М4 тоже найден и равен: М1М4 = (-2; -1; -4).
V = (1/6)(A1A2xA1A3)*A1A4.
М1М2xМ1М3 = 3 3 6
М1М4 = -2 -1 -4
-6 - 3 - 24 = -33.
V = (1/6)*|-33| = (33/6) = 11/2 = 5,5 куб. ед.
Длина высоты – это расстояние от точки D до плоскости АВС.
Для вычисления расстояния от точки M(Mx; My; Mz) до плоскости Ax + By + Cz + D = 0 используем формулу:
d = |A·Mx + B·My + C·Mz + D|/√(A² + B² + C²)
Значит, надо определить уравнение плоскости М1М2М3 по найденному нормальному вектору этой плоскости (он равен векторному произведению векторов М1М2 и М1М3, то есть (3; 3; 6)) и координатам точки M1( 1; 1; 2).
Подставляем эти данные в уравнение плоскости.
3(x – 1) + 3(y – 1) + 6(z – 2) = 0,
3x – 3 + 3y – 3 + 6z – 12 = 0,
3x + 3y + 6z – 18 = 0. Это уравнение плоскости М1М2М3.
Подставим в формулу данные: точка M4(-1; 0; -2) и координаты нормального вектора плоскости М1М2М3: (3; 3; 6).
d = |3·(-1) + 3·0 + 6·(-2) - 18|/√(3² + 3² + 6²) =
|-3 + 0 - 12 - 18|/√(9 + 9 + 36) = 33/√54 = 11√6/6 ≈ 4,491.
2.5. Встановити орієнтацію трійки векторів M1M2, M1M3 і M1M4.
Тройка векторов {a, b, c} является правой тогда и только тогда, когда смешанное произведение (a, b, c) этих векторов больше нуля; и левой – если смешанное произведение меньше нуля.
В пункте 2.4. смешанное произведение найдено и равно -33.
Значит, тройка векторов левая.