Предмет: Математика,
автор: vasyapupkin2681
Найдите корень уравнения 3^log9 2x+8=2
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Автор ответа:
0
Ответ:
Пошаговое объяснение:
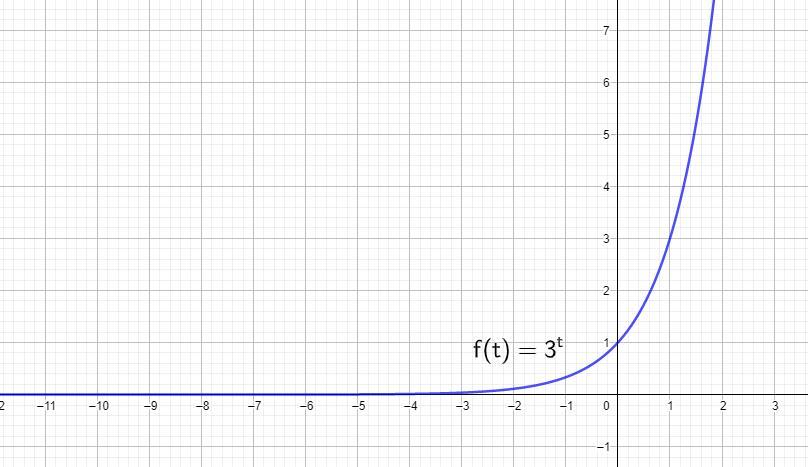
Пусть
Так как - показательная функция, то по свойствам показательной функции
, то есть показательная функция не может принимать отрицательные значения, тогда уравнение
не имеет корней, то есть
.
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ПеченюхаTv
Предмет: Русский язык,
автор: mashamindlina
Предмет: Русский язык,
автор: aимена
Предмет: Алгебра,
автор: kotya2727483817
Предмет: Алгебра,
автор: dezzmoo