Предмет: Математика,
автор: karineepikyan
Помогите пожалуйста
Приложения:
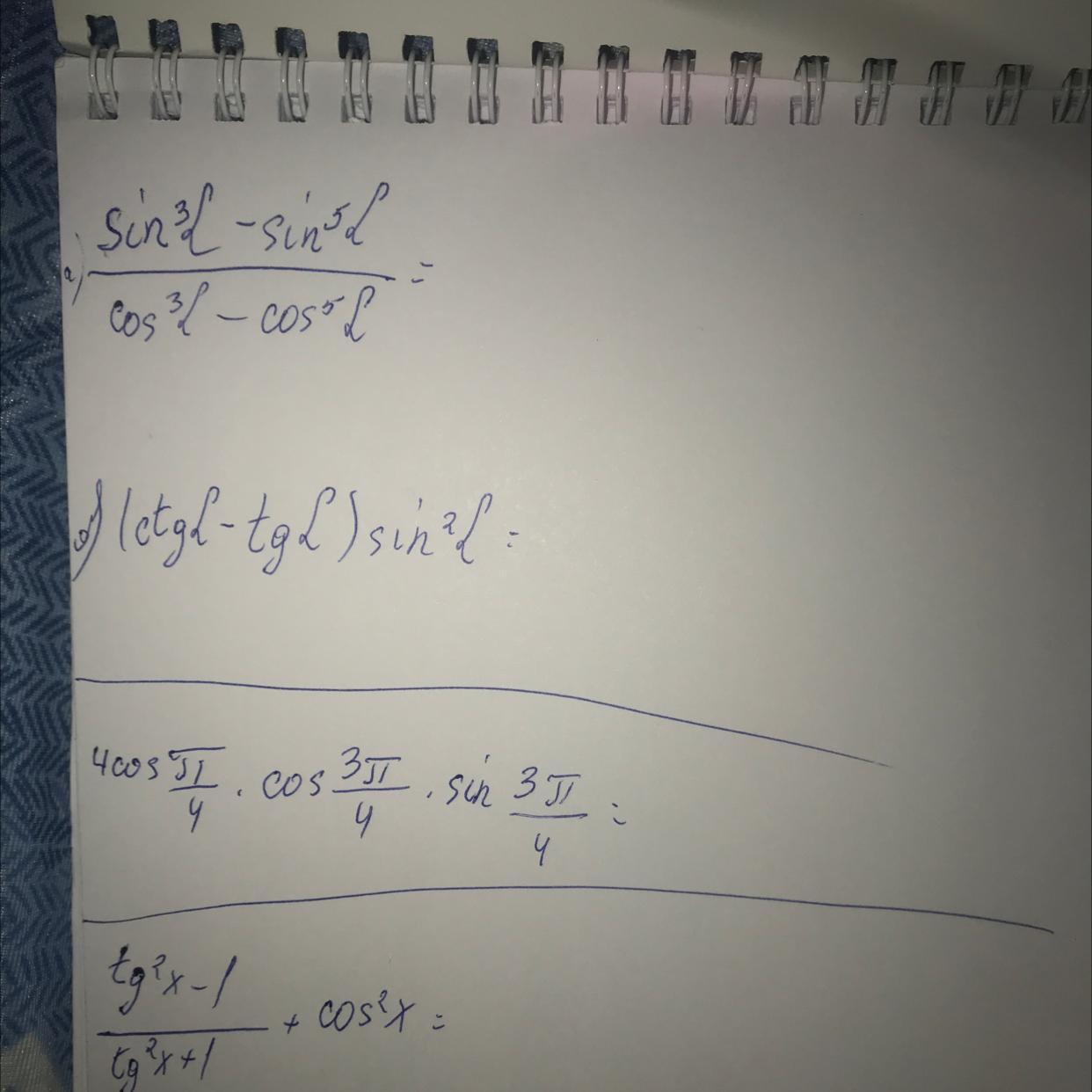
Vopoxov:
Не за что. Последний пока не решил
Ответы
Автор ответа:
2
Пошаговое объяснение:
1)
2)
3)
Спасибо
Похожие вопросы
Предмет: Русский язык,
автор: Dzhabaev02
Предмет: Русский язык,
автор: ниКотэйка
Предмет: Русский язык,
автор: TheGrishaPlays
Предмет: Алгебра,
автор: aleksa0053
Предмет: Русский язык,
автор: kakoitochel666