Предмет: Математика,
автор: xxiimaximmax
Помогите решить задание с пределом
Приложения:
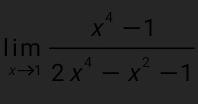
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: Shork123
Предмет: Английский язык,
автор: grunicheva2014
Предмет: Русский язык,
автор: умняшка90
Предмет: Алгебра,
автор: uukin51
Предмет: Алгебра,
автор: cat25251