Предмет: Алгебра,
автор: Shon2208
Перепишіть у вигляді раціонального дробу
Приложения:
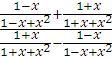
Ответы
Автор ответа:
2
Ответ:
Объяснение:
dDeVoChKa:
Добрый день! Если Вас не затруднит, решите, пожалуйста, задачку у меня в профиле. Заранее благодарю!
Похожие вопросы
Предмет: Русский язык,
автор: yanaamby
Предмет: Русский язык,
автор: igorevolckov
Предмет: Русский язык,
автор: Банан011
Предмет: Английский язык,
автор: nura20061
Предмет: Математика,
автор: 3213217