Предмет: Математика,
автор: Ternov21
помогите пожалуйста (4)
Приложения:

Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
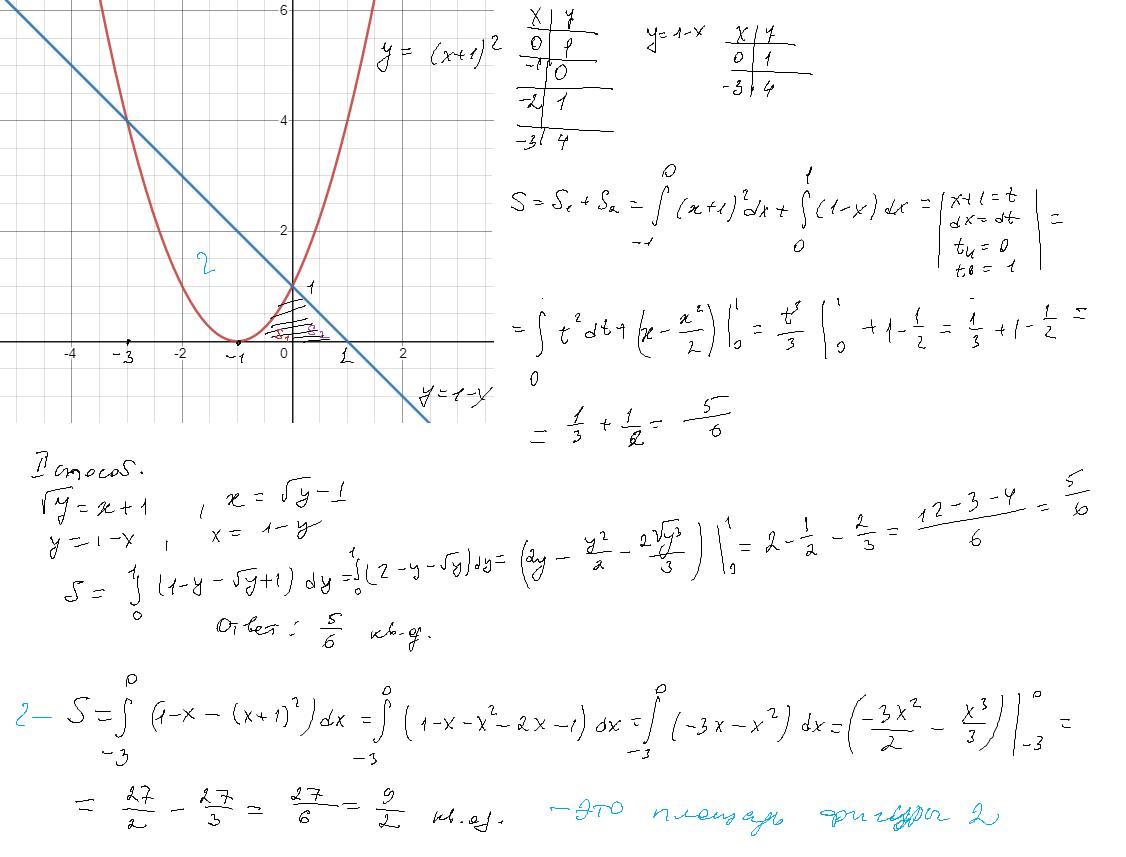
Если искать площадь ограниченную функциями и осьою Ох, то получается 5\6 кв.ед.
Но такого ответа нет.
Если искать площадь между функциями без последнего условия - оси Ох, то получается 9\2 кв.ед.
Получается, что к поставленной задаче ответа нет.
Приложения:
Автор ответа:
1
Ответ:
Пошаговое объяснение:
y=(x+1)²; y=1-x; ось 0х или у=0
Площадь найдем по формуле:
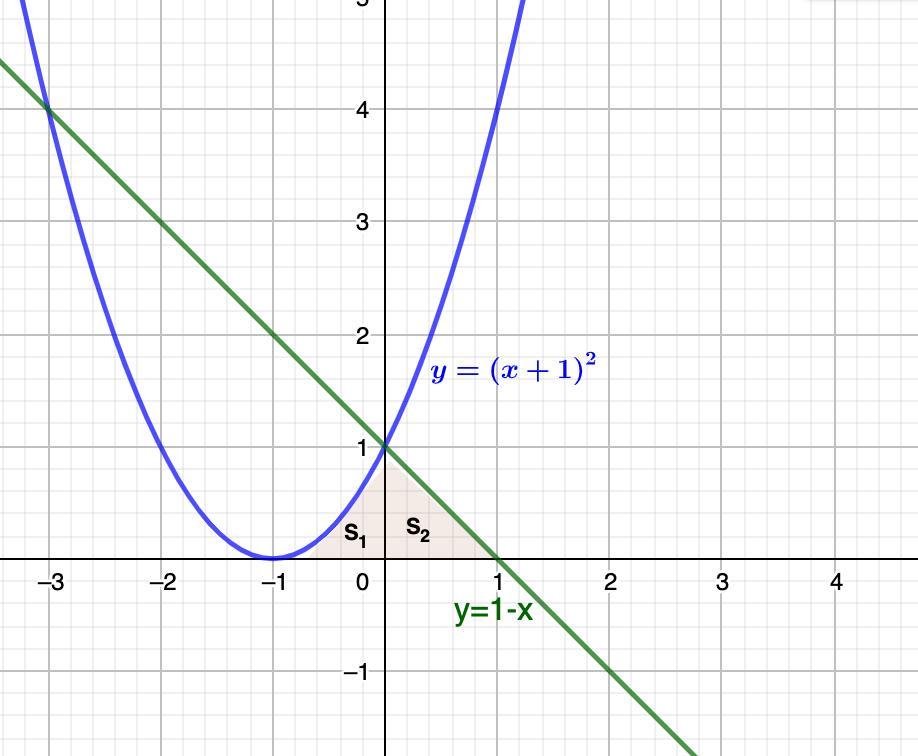
Рассмотрим чертеж:
Искомая площадь состоит из двух площадей (S₁ + S₂)
У S₁ :
У S₂ :
Найдем площадь:
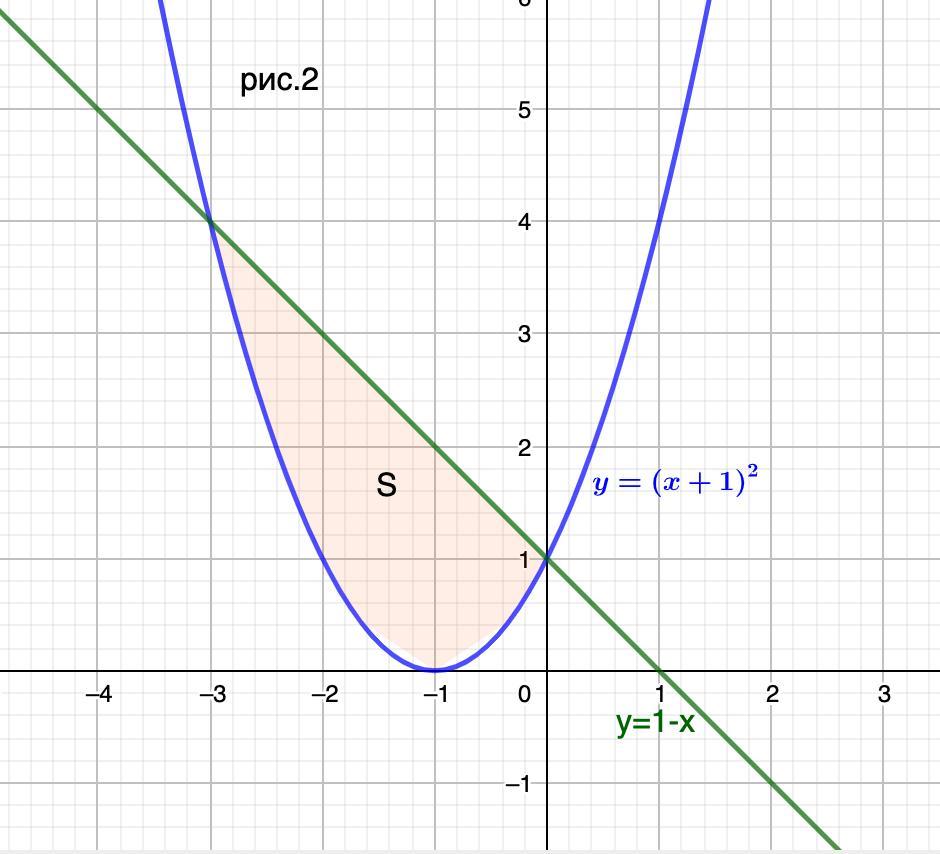
Данного ответа нет. Предположу что "и осью 0х" - лишнее. И тогда искомая площадь будет другая. (см. рис.2)
Тогда
Найдем площадь:
S= (ед²)
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: орловский3
Предмет: Українська мова,
автор: pirinets2000
Предмет: Русский язык,
автор: викуля158
Предмет: География,
автор: kristpog2010
Предмет: Алгебра,
автор: kargoxana123