Предмет: Алгебра,
автор: niceuraura
Решите неравенство:
(фото)
Приложения:
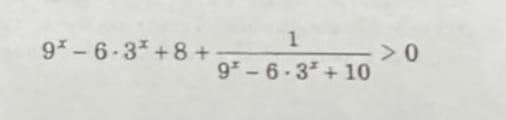
Ответы
Автор ответа:
0
Ответ:
Объяснение:
ODZ:
x∈R
Похожие вопросы
Предмет: Қазақ тiлi,
автор: AruArman
Предмет: Русский язык,
автор: жадный2
Предмет: Окружающий мир,
автор: Пушиcтая
Предмет: Математика,
автор: egoza1103
Предмет: Русский язык,
автор: eva2687