Предмет: Алгебра,
автор: eugeniodepez
Здравствуйте помогите решить задание по алгебре
даю 30 баллов
Решите систему неравенств:
Приложения:
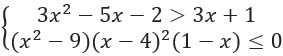
Karinca2376190:
Неееет
блин
я такое не знаю
прости мы еще такое не изучали
а так бы я бы помогла....
●︿●
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Спасибо большое!!!
Автор ответа:
1
решаем методом интервалов
_+___ -1/3 __-____3___+___
ответ на решение первого неравенства (-oo;-1/3) (3;+oo)
решаем методом интервалов
_+__ -3__-__1_+_3_ -__4__-__
ответ на решение второго неравенства [-3;1] [3;+oo)
общее решение это пересечение промежутков
[-3;-1/3) (3;+oo)
Cпасибо большое!!!
Похожие вопросы
Предмет: Русский язык,
автор: Fkkk
Предмет: Английский язык,
автор: жека225
Предмет: Русский язык,
автор: нико41
Предмет: Математика,
автор: bich15