Предмет: Геометрия,
автор: elizarovarseny72
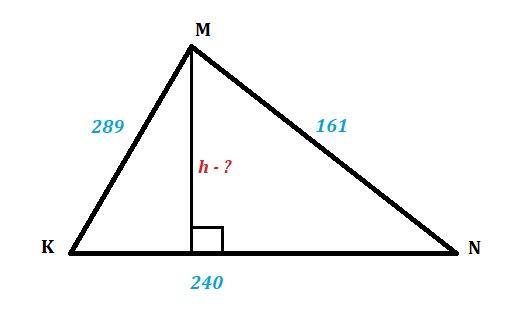
Чему равна высота, опущенная к стороне NK NK треугольника MNKMNK , если MN= 161MN=161 , NK=240NK=240 , KM = 289KM=289 ?
Ответы
Автор ответа:
3
Ответ:
h = 161
Объяснение:
Найдём площадь треугольника по формуле Герона:
, где a,b,c - стороны треугольника, р - полупериметр.
С другой стороны, Площадь треугольника равна произведению половины основания треугольника (a) на его высоту (h), проведенную к основанию:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: hoholkobghkobuu
Предмет: Английский язык,
автор: саня716674
Предмет: Русский язык,
автор: катя2872
Предмет: Математика,
автор: 01DaNiiL10
Предмет: Русский язык,
автор: stepa31032006