Предмет: Алгебра,
автор: evgenijsokolov92475
математика помогите пожалуйста
80 балов даю
Приложения:
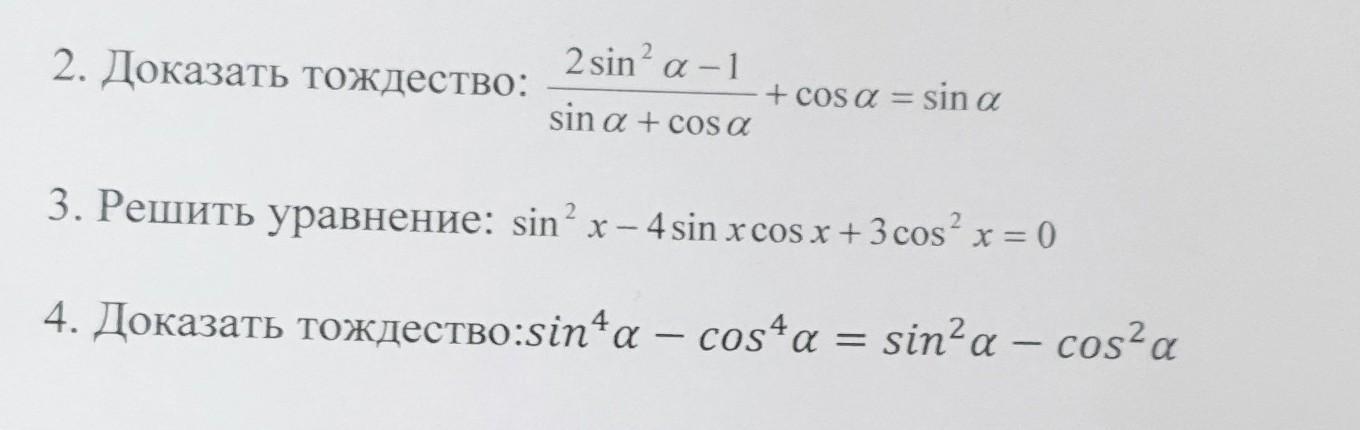
Ответы
Автор ответа:
1
Объяснение:
2.3.
Ответ: x₁=π/4+πn, x₂=arctg(3)+πn.
4.
evgenijsokolov92475:
спасибо большое
Удачи.
Похожие вопросы
Предмет: Русский язык,
автор: yanaprosto
Предмет: Русский язык,
автор: 738587
Предмет: Английский язык,
автор: катя2826
Предмет: Қазақ тiлi,
автор: kot5298
Предмет: Русский язык,
автор: mbazarbekova56