Question

Помогите пж. Задание на скрине

Answer 1

Ответ:

Объяснение:

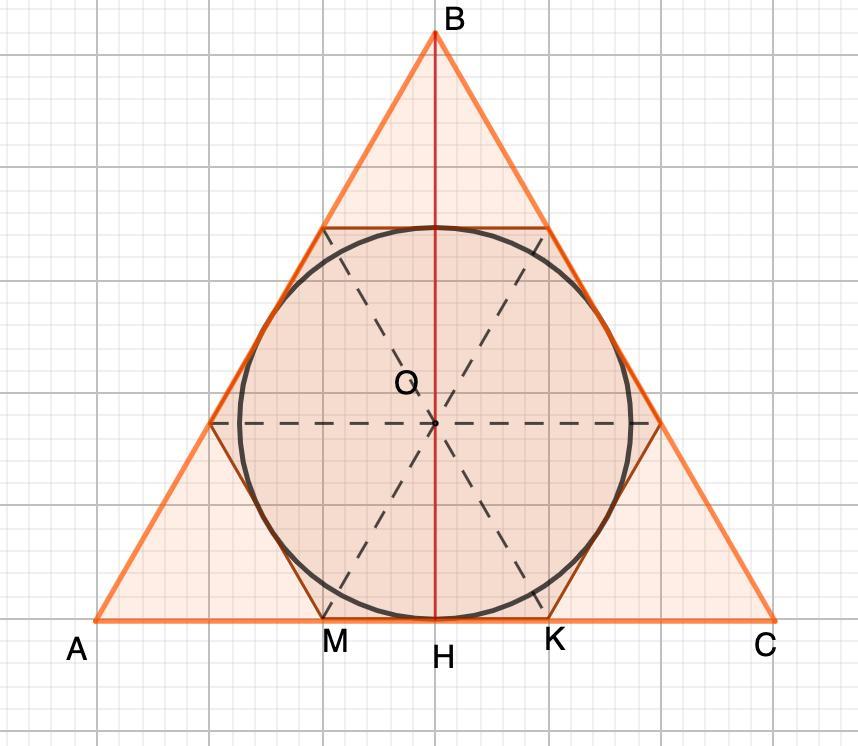
Дано: Правильный шестиугольник.

Окр. О - вписанная.

ΔАВС - равносторонний, описанный.

МК - 3√3 см.

Найти: S (ΔFDC)

Решение:

• Диагонали правильного шестиугольника пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной окружности.

⇒ ΔМКО - равносторонний, ОН - радиус вписанной окружности.

Высоту равностороннего треугольника можем найти по формуле:

$\displaystyle h=\frac{a\sqrt{3} }{2}$ , где а - сторона треугольника.

Рассмотрим ΔОМК - равносторонний.

$\displaystyle OH=\frac{MK*\sqrt{3} }{2}=\frac{3\sqrt{3}*\sqrt{3} }{2}=\frac{9}{2}\;_{(CM)}$

Рассмотрим ΔАВС - равносторонний.

Зная радиус вписанной окружности, найдем площадь по формуле:

$\displaystyle S=3\sqrt{3}\;r^2$

⇒

$\displaystyle S_{ABC}=3\sqrt{3}*(\frac{9}{2} ) ^2=\frac{243\sqrt{3} }{4}\;_{(CM^2)}$