Question

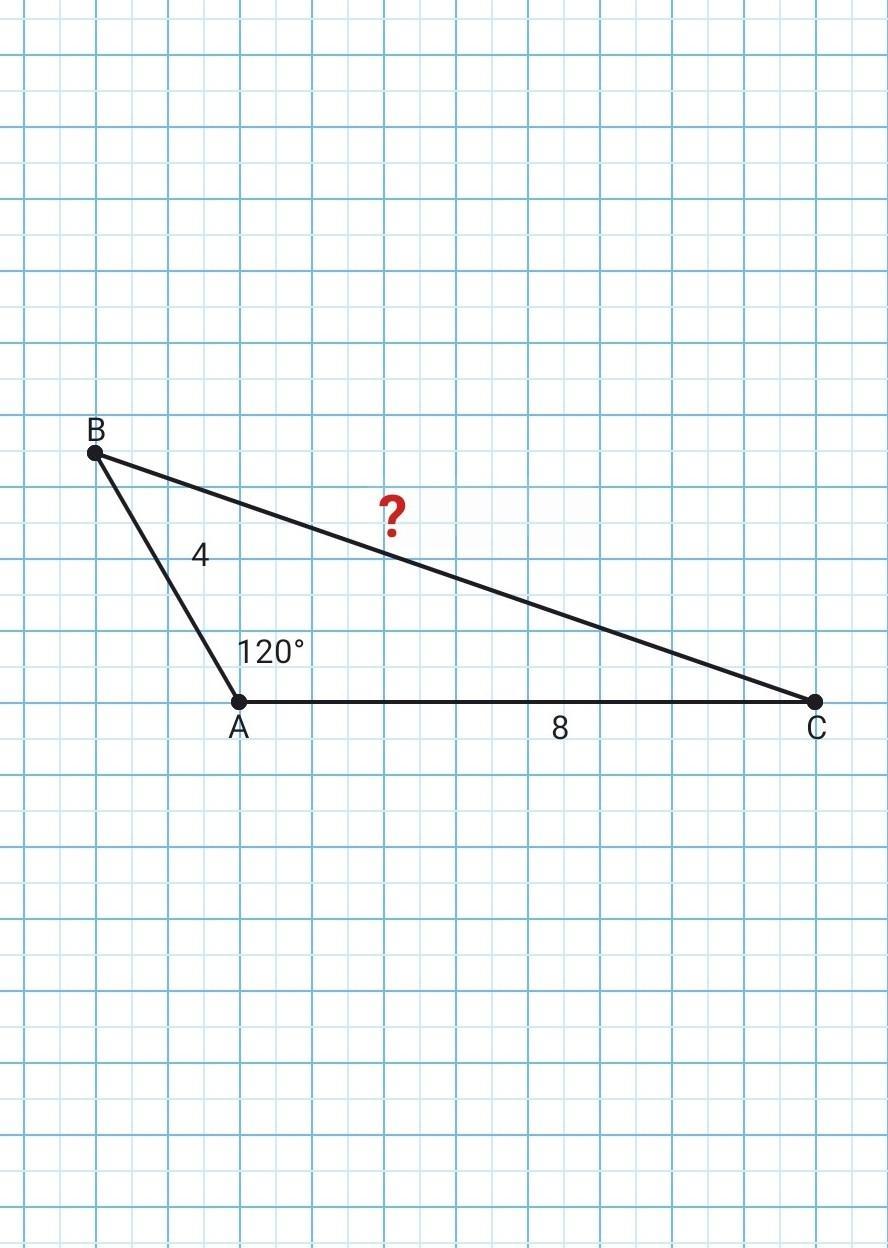
Есть треугольник ABC дано что АВ=4 AC=8 кут А= 120 .Найти S и ВС

Answer 1

Ответ:

S=

$8 \sqrt{3}$

кв.см

ВС=

$4 \sqrt{7}$

см

Объяснение:

• Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними.

S= 0.5× a×b×sin a

$s = \dfrac{1}{2} \times 4 \times 8 \times \sin(120) = \\ = 16 \times \dfrac{ \sqrt{3} }{2} = 8 \sqrt{3}$

По теореме косинусов найдём сторону BC.

• Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

${BC}^{2} = {AB}^{2} + {AC}^{2} - 2 \times AB \times BC \times \cos(120) = \\ = {4}^{2} + {8}^{2} - 2 \times 4 \times 8 \times ( - \frac{1}{2} ) = \\ = 16 + 64 + 32= 112 \\ \\ BC = \sqrt{112} = 4 \sqrt{7}$