Предмет: Алгебра,
автор: zakharmorozenko
ПОМОГИТЕ никак не могу решить.
Приложения:
Ответы
Автор ответа:
1
Ответ:
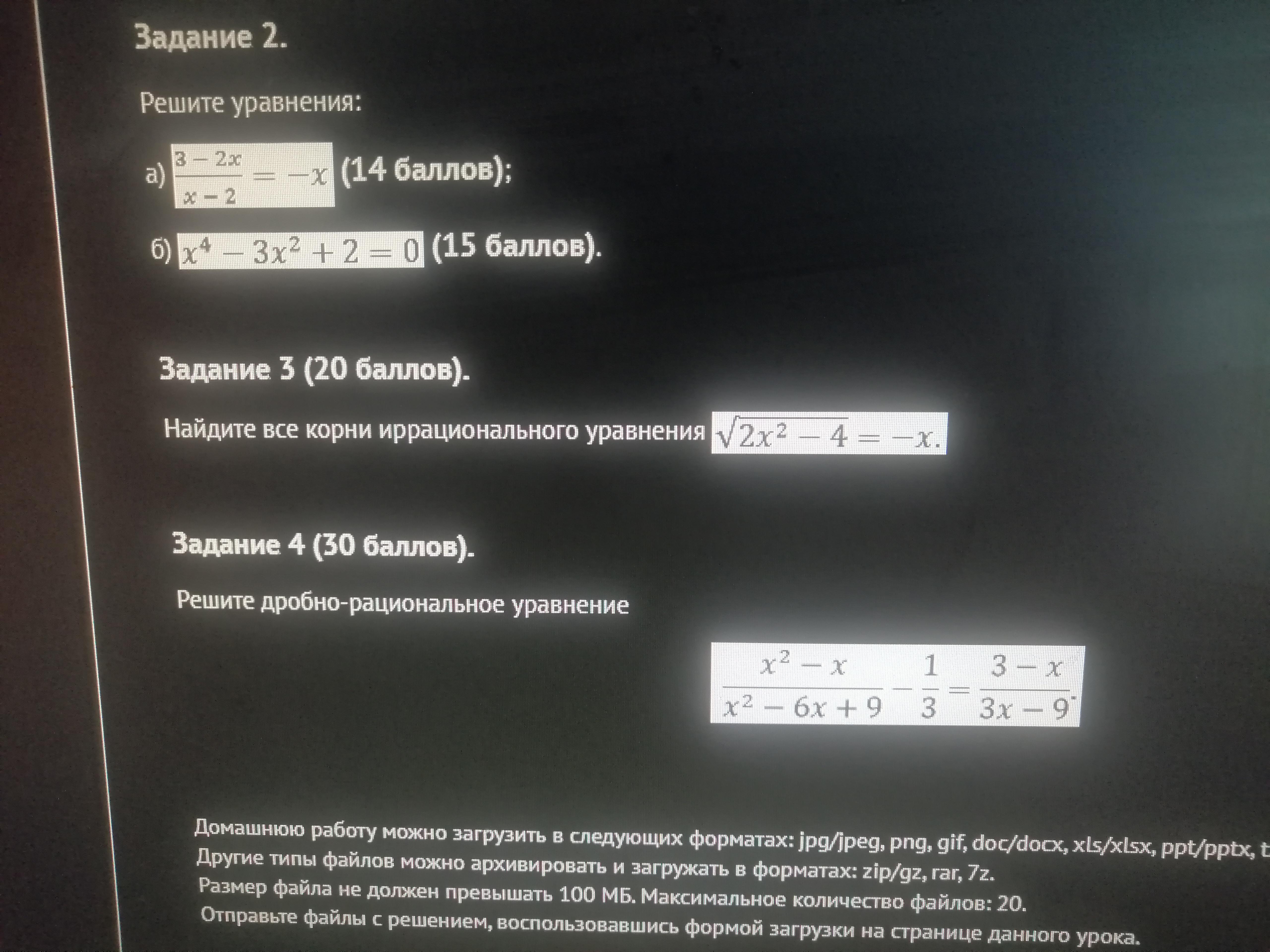
Задание 2.
а)
б)
Задание 3.
Задание 4.
Объяснение:
Задание 2.
а)
ОДЗ:
б)
Замена:
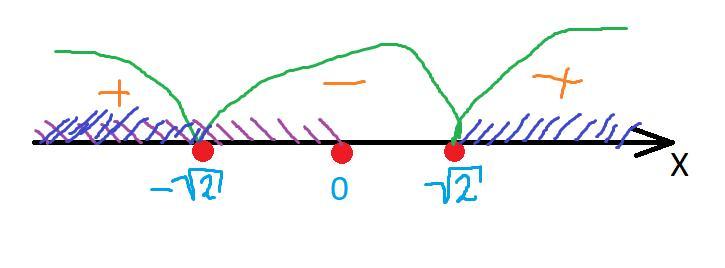
Задание 3.
ОДЗ:
- не входит в ОДЗ
Задание 4.
ОДЗ:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: nikitos1919
Предмет: Русский язык,
автор: David20131
Предмет: Другие предметы,
автор: lipaPROOOOD
Предмет: Физика,
автор: akupan