Предмет: Алгебра,
автор: Gerten
Даю 100 баллов, помогите решить
Приложения:
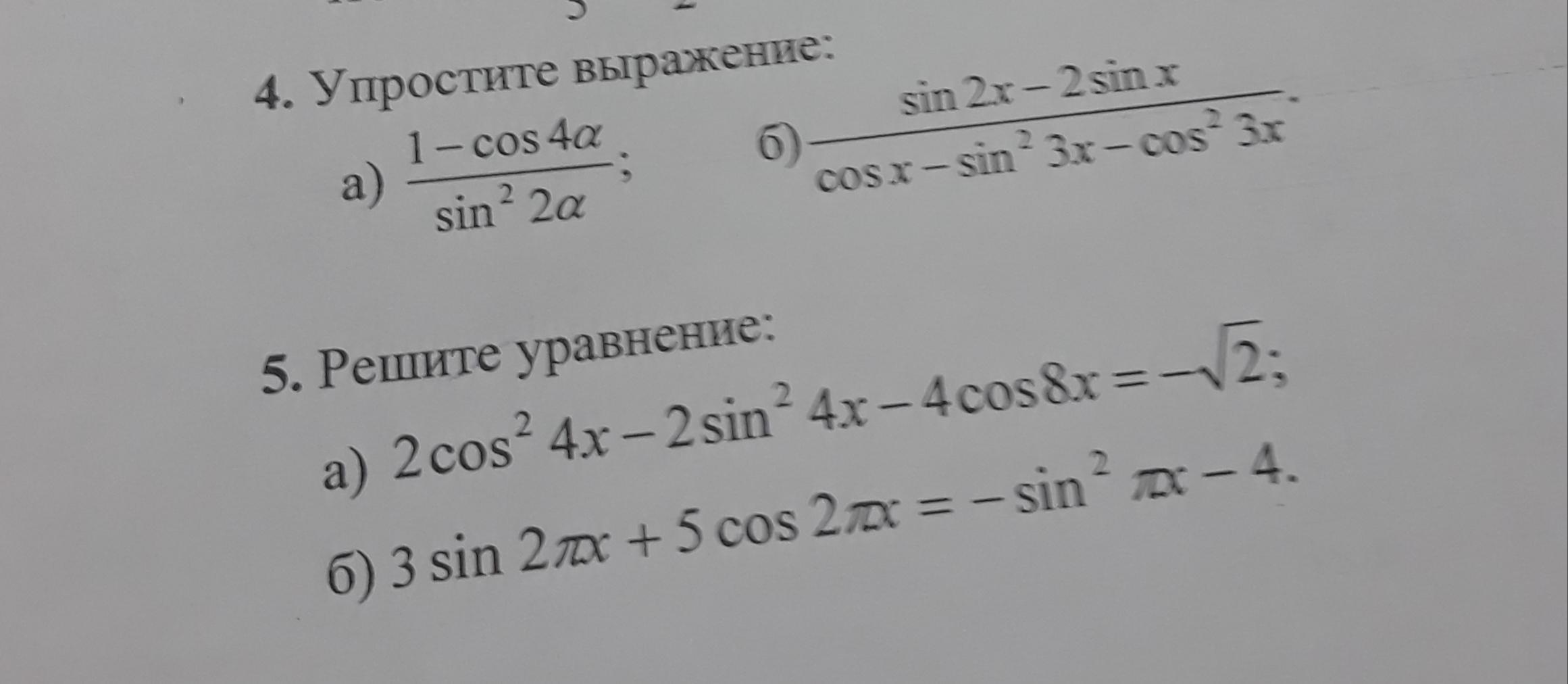
Gerten:
Срочно
Ответы
Автор ответа:
1
Ответ:
4.
а)
б)
5.
а)
б)
Объяснение:
4.
а)
б)
5.
а)
б)
Замена:
Похожие вопросы
Предмет: Окружающий мир,
автор: klochcov11
Предмет: Немецкий язык,
автор: Аноним
Предмет: Английский язык,
автор: stramilov03
Предмет: Биология,
автор: Masamedvedyeva12
Предмет: Русский язык,
автор: Аноним