Предмет: Алгебра,
автор: srrrij300
решить логарифмическое неравенство по примеру(пример на 2 фото)
Приложения:
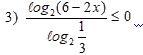

Ответы
Автор ответа:
1
Объяснение:
ОДЗ:
6-2x>0
-2x>-6
x<3
log2(1/3) меньше нуля => чтобы неравенство выполнялось необходимо, чтобы числитель был больше или равен нулю =>
Ответ: x ∈ (-∞; 2.5]
Автор ответа:
1
т.к. ㏒₂(1/3)<0, то ㏒₂(6-2х)≥0, решаем неравенство, применяя определение логарифма, 6-2х≥2⁰; 6-2х≥1; 2х≤5; х≤2.5; определяем ОДЗ, решая неравенство 6-2х>0, -2х>-6; х <3;
в итоге х∈(-∞; 2.5] -решение данного неравенства
Ответ х∈(-∞; 2.5]
Аноним:
Спасибо!!! АНТ я заметила))
Похожие вопросы
Предмет: Русский язык,
автор: voytyuknatalya
Предмет: Русский язык,
автор: swetlana2013
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: nurki11
Предмет: Қазақ тiлi,
автор: ПомошникГена