Предмет: Алгебра,
автор: maryna39
Помогите, срочно, пж!!!
Решить уравнение
Приложения:
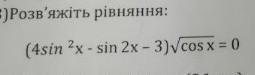
Ответы
Автор ответа:
1
с учетом ОДЗ:
овтет:
maryna39:
Спасибо!
Можешь помочь еще пж?
Похожие вопросы
Предмет: Другие предметы,
автор: lera472
Предмет: Русский язык,
автор: Squash120
Предмет: Русский язык,
автор: AlexandraAleks
Предмет: Английский язык,
автор: dkdkdjfhhd
Предмет: Математика,
автор: volgodeloovy2y2