Предмет: Алгебра,
автор: villiwonkka1
N19
_._._._._._..__.
Приложения:

Ответы
Автор ответа:
1
Объяснение:
5)
Подставим координаты точки А и найдем С:
⇒
6)
Найдем С:
7)
Найдем С:
⇒
8)
Найдем С:
⇒
Приложения:
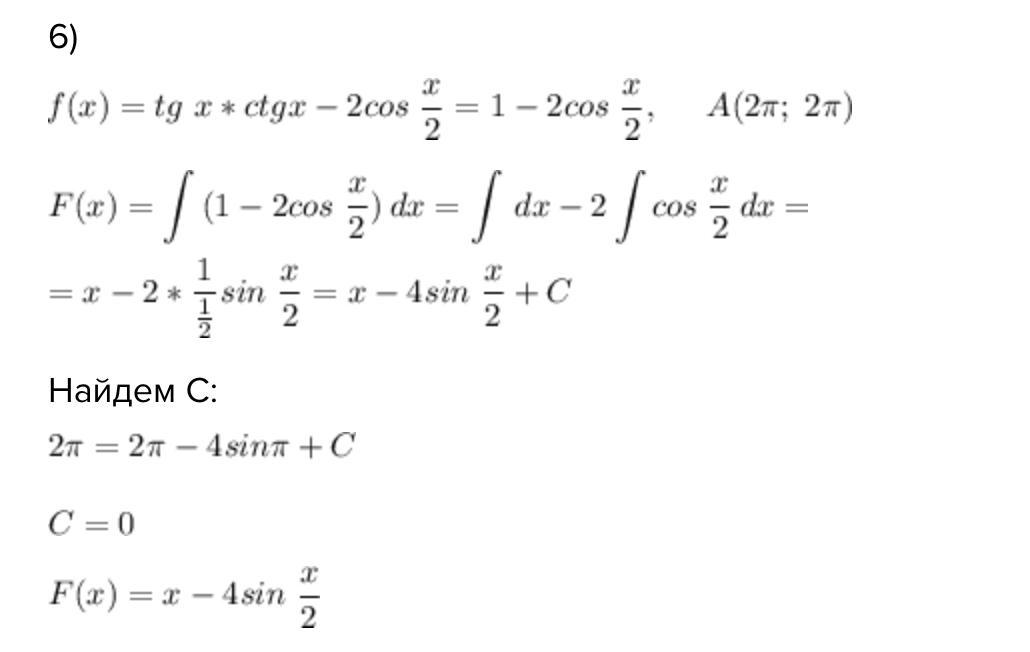

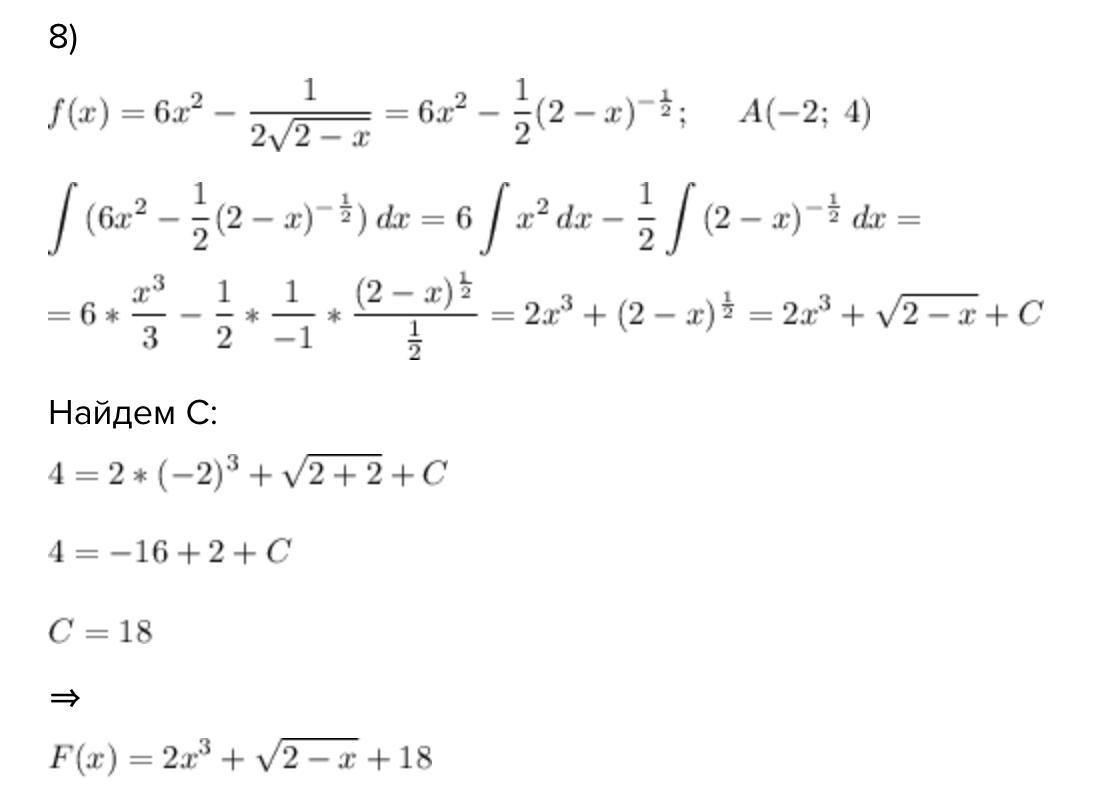
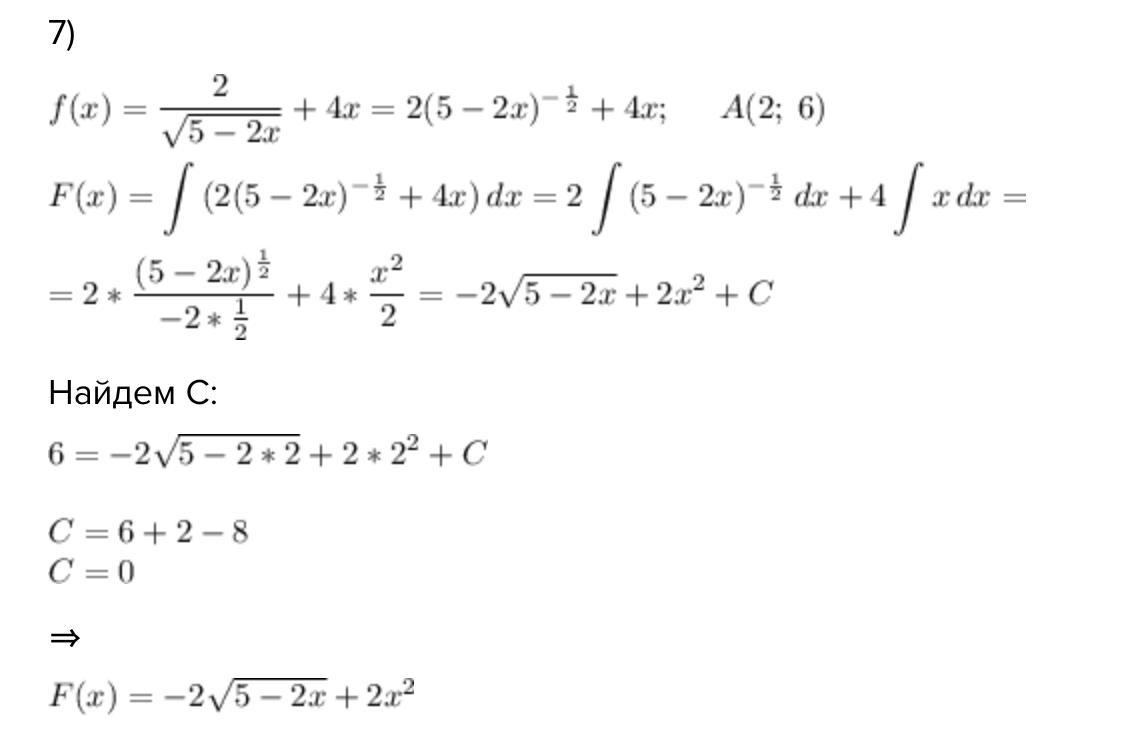
villiwonkka1:
спасибо большое
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: madmax060804
Предмет: Английский язык,
автор: adamelena
Предмет: Математика,
автор: 228KUROPATOCHKA228
Предмет: Математика,
автор: sofiya3682