Предмет: Математика,
автор: Аноним
Найти угол между градиентами функций u (x, y, z) и v (x, y, z) в точке М
Приложения:
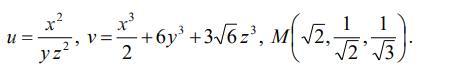
Ответы
Автор ответа:
3
Находим частные производные первого порядка функции трёх переменных u
по х: 2х/(уz²); по у: -x²/(y²z²); по z: -2х²/(уz³);
получаем (2х/(уz²))*→i+ ( -x²/(y²z²))*→j -(2х²/(уz³))*→k; подставляем координаты точки М ,получаем 12*→i-12*→j -12√6*→k;
Аналогично находим частные производные первого порядка функции трёх переменных v:
по х: 3х²/2; по у: 18y²; по z: 9√6z²; подставляем координаты точки М ,получаем 3→i+9*→j +3√6*→k;
найдем скалярное произведение полученных векторов
12*3-12*9 -12√6*3√6=36-108-216=-288;
√(144+144+144*6)=12√8=24√2
и √(9+81+9*6)=√144=12
cosα=-288/(24√2*12)=-12/(12√2)=-1/(√2)=-√2/2, значит, угол между векторами равен 180°-45°=135°
Аноним:
спасибо большое!
отлично решаете
ant20202020
ant20202020
помогииитее
пжж
Похожие вопросы
Предмет: Русский язык,
автор: AlenXhelen
Предмет: Русский язык,
автор: anastasiiazhuk3Nasta
Предмет: Українська мова,
автор: AKozko
Предмет: Химия,
автор: vsivas
Предмет: История,
автор: ВиолеттаЦветкова