ПОЖАЛУЙСТА ПОМОГИТЕ С МАТЕМАТИКОЙ ПОЖАЛУЙСТА
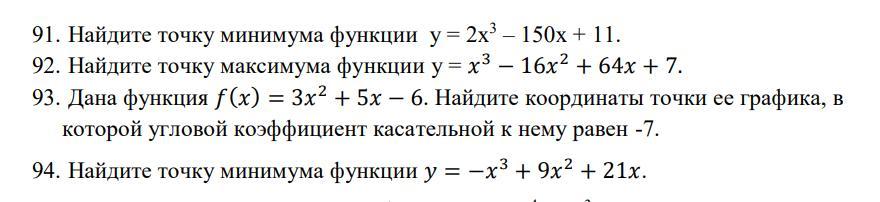
Ответы
91) Дана функция y = 2x³ - 150x + 11.
Производная равна y’ = 6x² - 150.
Приравниваем её нулю: 6x² - 150 = 0, x² = 150/6 = 25, х = +-5.
Найдены 2 критические точки: х = -5 и х = 5.
Находим значения производной вблизи этих точек.
х = -6 -5 -4 4 5 6
y’ = 66 0 -54 -54 0 66.
Как видим, минимум находится в точке х = 5 (производная меняет знак с минуса на плюс).
92) Дана функция y = x³ - 16x² + 64x + 7.
Производная равна y’ = 2x² - 16x + 64
Приравниваем её нулю: 2x² - 16x + 64 = 0 или x² - 18x + 32 = 0,
Ищем дискриминант:
D=(-18)^2-4*1*32=324-4*32=324-128=196;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√196-(-18))/(2*1)=(14-(-18))/2=(14+18)/2=32/2=16;
x_2=(-√196-(-18))/(2*1)=(-14-(-18))/2=(-14+18)/2=4/2=2.
Найдены 2 критические точки: х = 2 и х = 16.
Находим значения производной вблизи этих точек.
х = 1 2 3 15 16 17
y’ = 15 0 -13 -13 0 15
Как видим, максимум находится в точке х = 2 (производная меняет знак с плюса на минус).
93) Дана функция y = 3x² + 5x - 6.
Производная равна y’ = 6x + 5.
Угловой коэффициент касательной к графику функции равен производной этой функции.
Приравниваем 6х + 5 = -7, отсюда х = (-7 – 5)/6 = -12/6 = -2.
Найдена одна точка х = -2, в которой угловой коэффициент касательной к графику функции равен -7.
94) Дана функция y = -x³ + 9x² + 21x.
Производная равна y’ = -3x² + 18x + 21.
Приравниваем её нулю: -3x² + 18x + 21 = 0 или x² - 6x - 7 = 0,
Ищем дискриминант:
D=(-6)^2-4*1*(-7)=36-4*(-7)=36-(-4*7)=36-(-28)=36+28=64;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√64-(-6))/(2*1)=(8-(-6))/2=(8+6)/2=14/2=7;
x_2=(-√64-(-6))/(2*1)=(-8-(-6))/2=(-8+6)/2=-2/2=-1.
Найдены 2 критические точки: х = -1 и х = 7.
Находим значения производной вблизи этих точек.
х = -2 -1 0 6 7 8
y’ = 9 0 -7 -7 0 9
Как видим, минимум находится в точке х = 7 (производная меняет знак с минуса на плюс).