Question

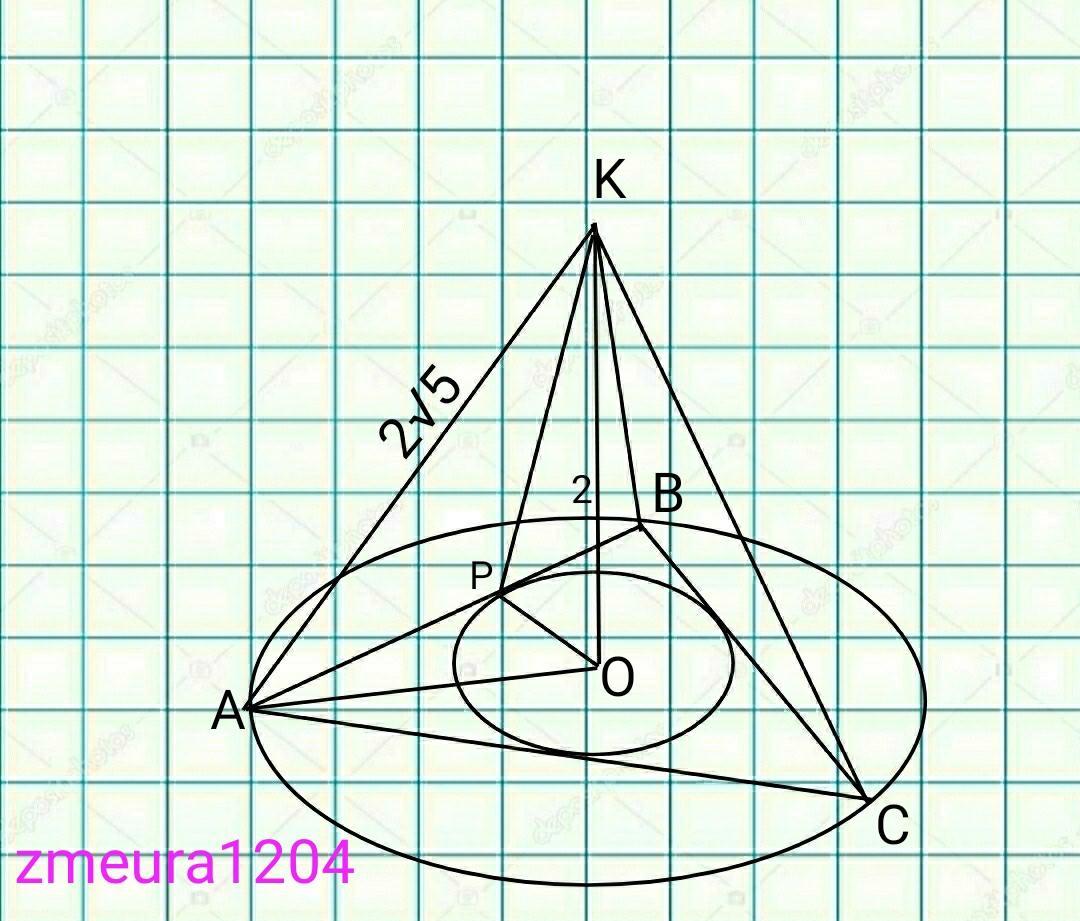
высота правильной треугольной пирамиды равна 2 а ее боковое ребро равно 2 корень из 5 найдите объем пирамиды, боковую поаерхность пирамиды, двугранный угол при основании пирамиды

Answer 1

Ответ:

V=8√3 ед³

Sбок=12√6 ед²

<КРО=45°

Объяснение:

∆АОК- прямоугольный треугольник

По теореме Пифагора

АО=√(АК²-КО²)=√((2√5)²-2²)=√(20-4)=

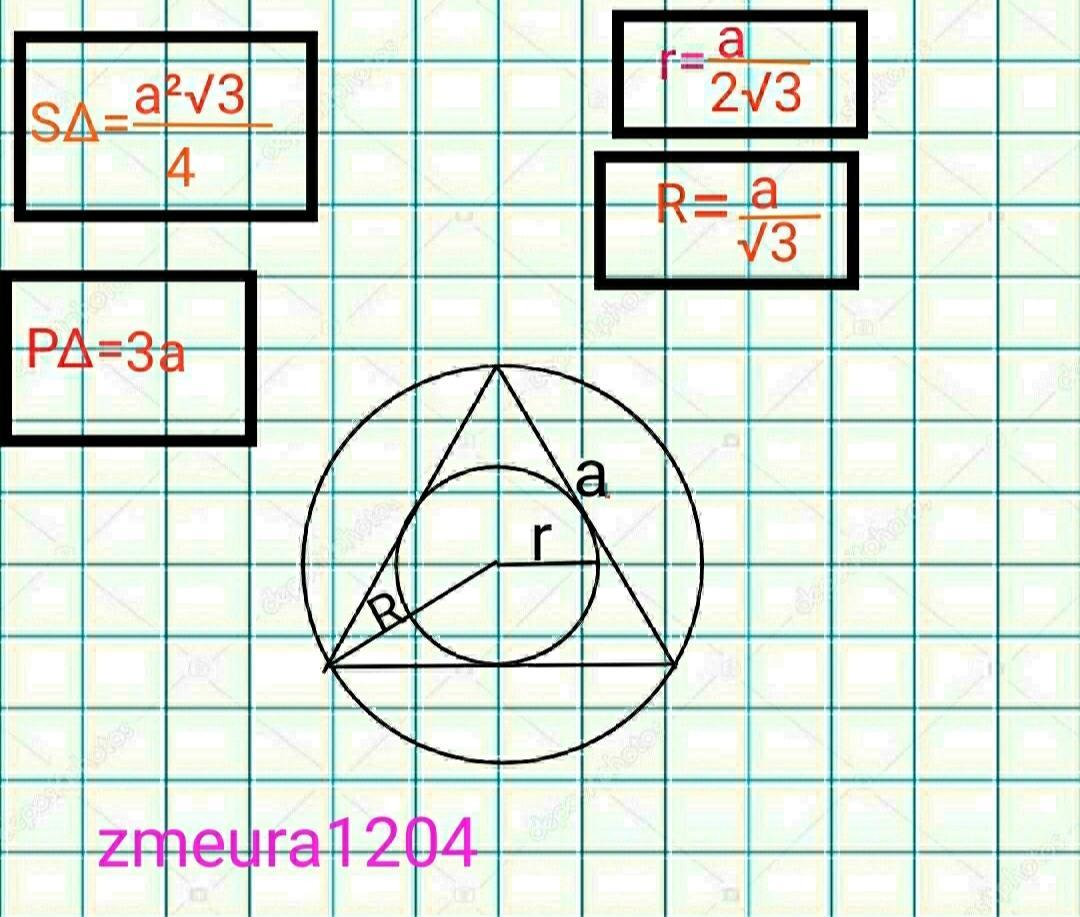
=√16=4 ед радиус описанной окружности равностороннего треугольника в основании.

АВ=АО*√3=4√3 ед сторона треугольника основания.

Sосн=АВ²√3/4=(4√3)²√3/4=12√3 ед²

V=1/3*Sосн*h, где h=KO=2ед

V=1/3*12√3*2=8√3 ед³

AO:PO=2:1. (R:r=2:1)

PO=AO:2=4:2=2 ед радиус вписанной окружности в основание.

∆РОК- прямоугольный треугольник

По теореме Пифагора

КР=√(КО²+РО²)=√(2²+2²)=2√2 ед апофема пирамиды

Росн=3*АВ=3*4√3=12√3 ед. периметр основания.

Sбок=1/2*КР*Росн=1/2*2√2*12√3=12√6 ед²

<КРО- двугранный угол.

tg<KPO=KP/PO=2/2=1

<KPO=45°