Предмет: Алгебра,
автор: ggfgyyff5655
Нужна срочная помощь с Алгеброй, 11 класс!!!
Приложения:
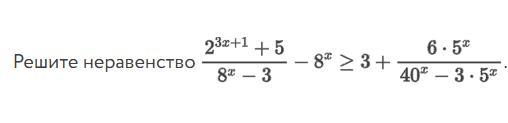
Ответы
Автор ответа:
1
решаем методом интервалов
____-2____(0)__+___(3)_-_4__+__
обратная замена
ответ:
Автор ответа:
0
- - - - - [ - 2] + + + + + (3) - - - - - [4] + + + + + m
/////////////// //////////////
Похожие вопросы
Предмет: Русский язык,
автор: darkkate1
Предмет: Английский язык,
автор: sve305
Предмет: Окружающий мир,
автор: сокол38
Предмет: Русский язык,
автор: vchupov
Предмет: Обществознание,
автор: AntonAV