Question

ПРОШУУУ ДАЮ 50 баллов
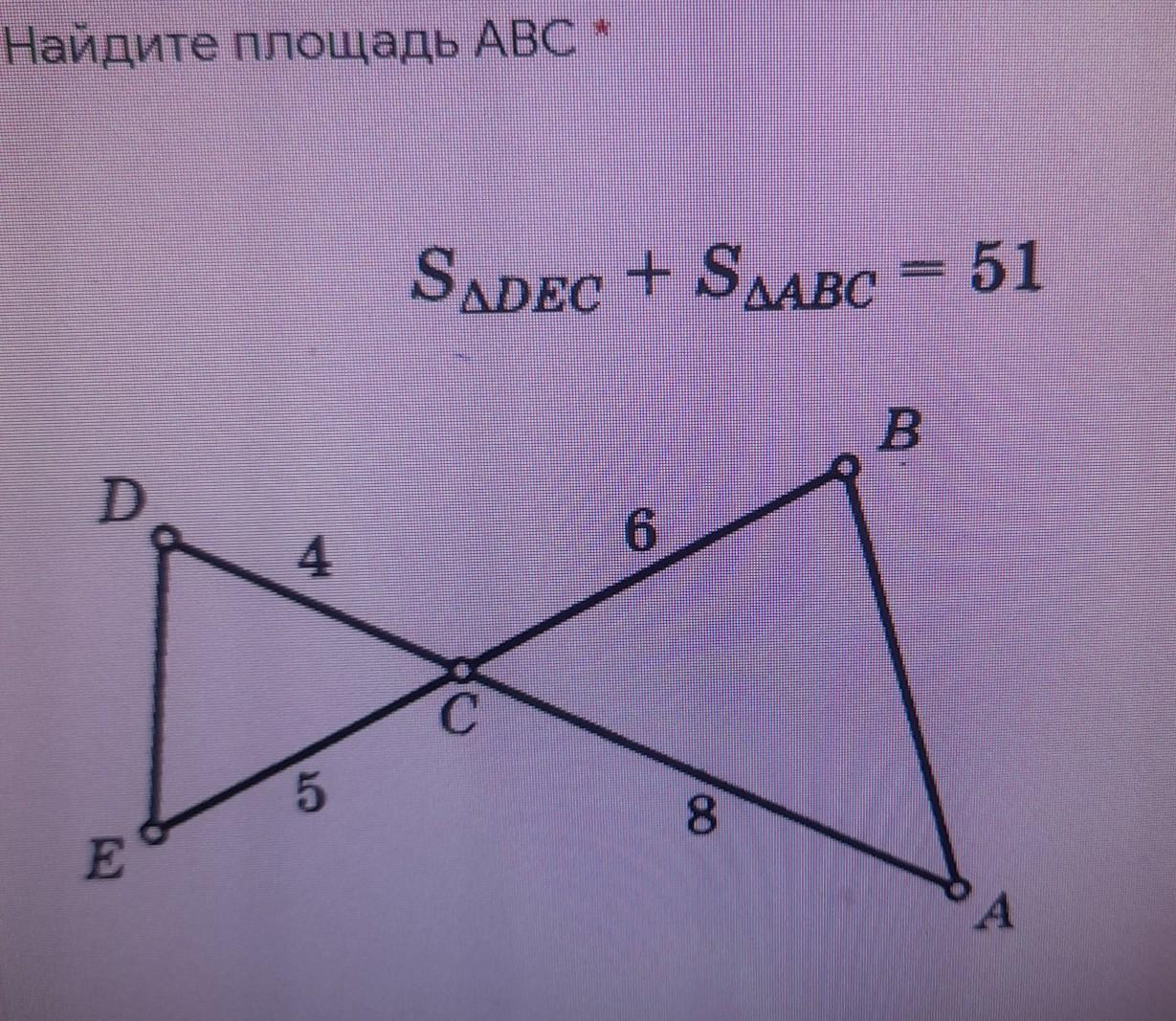
Отрезки AD и BE пересекаются в точке C. EC = 5, DC = 4, CB = 6, CA = 8. SΔDEC + SΔABC=51​

Answer 1

По теореме об отношении площадей, имеющих по равному углу имеем

S(ABC) :S(DCE) =(CB*CA) :(CE*CD) ,

S(ABC) : (51-S(ABC) )=(6*8) :(5*4) ,

S(ABC) : (51-S(ABC) )=12:5,

5*S(ABC) =12*(51-S(ABC) )

17*S(ABC) =12*51=> S(ABC) =36 ед²

Answer 2

Ответ:

Короче есть формула S=(a*b*sin<C)/2

У этих треугольников вершины вертикальна равны а значит S∆DEC +S∆ABC=51. а и b это как 4,5 или 6,8

После S∆DEC=(4*5*sin<C)/2

S∆ABC=(6*8*sin<C)/2 после исходя из этого получаем (4*5*sin<C)/2 + (6*8*sin<C)/2=51. Из этого 10*sin<C + 24 sin<C = 51 а значит sin<C =51/34

Найдем площадь ABC = (6*8*51/34)/2=это будет ответ 36 см²

Объяснение: