Предмет: Алгебра,
автор: Nurzhan94
вычислите ...............................
Приложения:
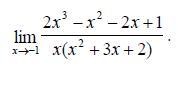
Ответы
Автор ответа:
0
Объяснение:
Вроде так)). Рад был помочь
Приложения:

Автор ответа:
0
Ответ:
Находим пределы числителя и знаменателя:
Так как 0/0 является неопределенностью, преобразуем выражение:
Предел равен -6
Похожие вопросы
Предмет: Английский язык,
автор: джеси4
Предмет: Українська мова,
автор: annAsoboleva05
Предмет: Русский язык,
автор: Алиса9463
Предмет: Русский язык,
автор: pomogator93
Предмет: Немецкий язык,
автор: kate444ka00