Предмет: Алгебра,
автор: ivanov2021de
Найти производную, помогите пожалуйста
Приложения:
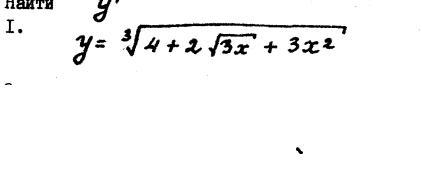
Ответы
Автор ответа:
2
Ответ:
Автор ответа:
0
у'=((4+2√(3x)+3x²)¹/³)'=(1/3)*(4+2√(3x)+3x²))⁻²/³)*(4+2√(3x)+3x²)'=
(1/(3*(4+2√(3x)+3x²)²/³)*(2*3/(2√(3x))+6x)=
(1/(3*(4+2√(3x)+3x²)²/³)*(3/(√(3x))+6x);
Universalka:
Зато у вас не решение , а абракадабра какая-то .
Похожие вопросы
Предмет: Английский язык,
автор: aminka12а
Предмет: Русский язык,
автор: Nastua331
Предмет: Русский язык,
автор: olga504
Предмет: Литература,
автор: nastyatravinina