Предмет: Алгебра,
автор: obsessionjekyl
Найти производные первого порядка данных функций.
Приложения:
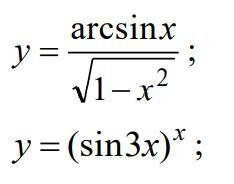
Ответы
Автор ответа:
1
1.
2.
Похожие вопросы
Предмет: Українська мова,
автор: olgaannesannate
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: Елизавета19992000
Предмет: Физика,
автор: EliteShank
Предмет: Геометрия,
автор: Лисса11111