Предмет: Геометрия,
автор: rozockarozocka20
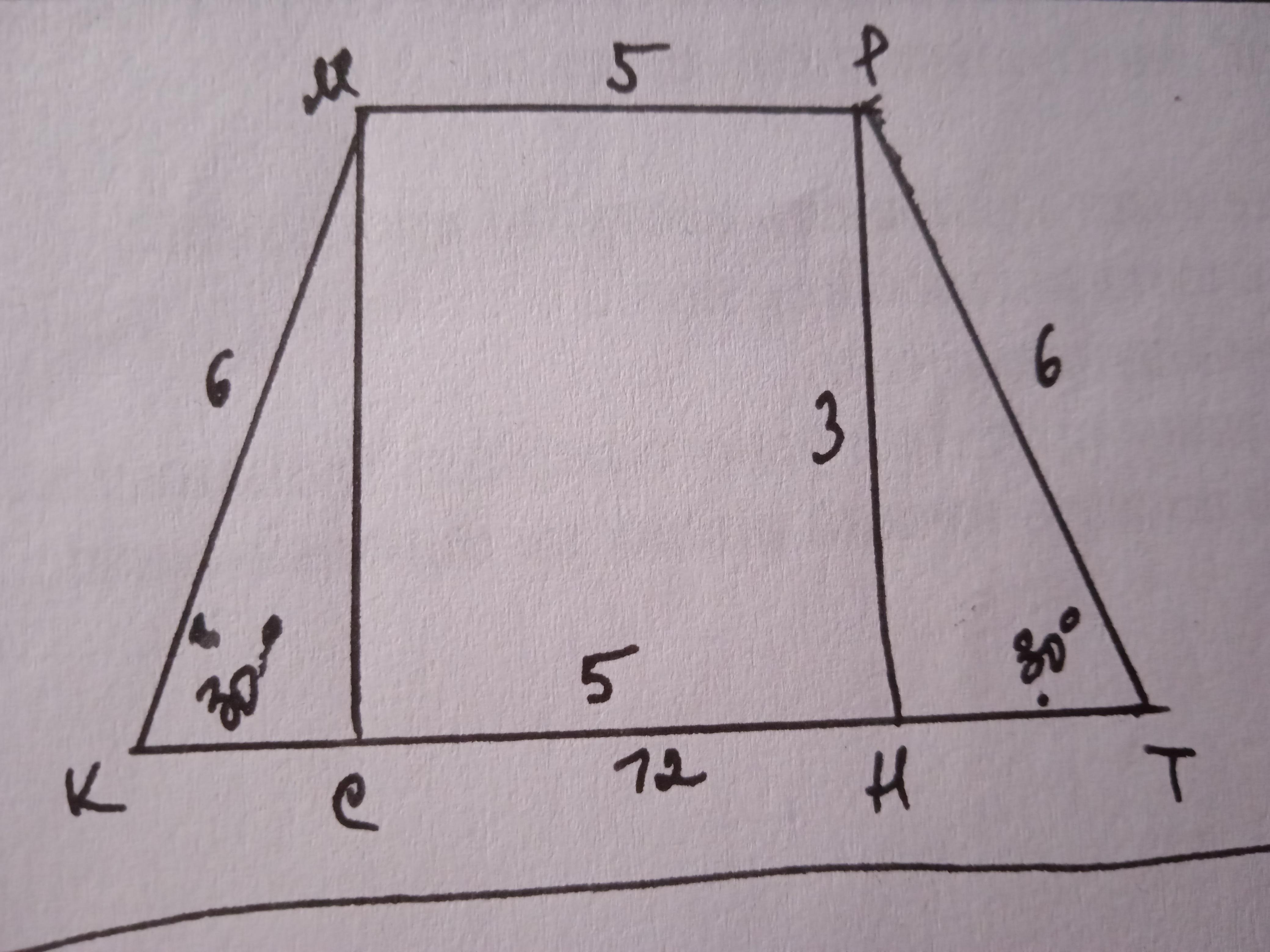
в равнобедренной трапеции основания равны 5и 12, боковая сторона 6см, а острый угол - и 30°, вычислите площадь трапеции
Ответы
Автор ответа:
0
Ответ:
25,5 см²
Объяснение:
Дано: КМРТ - трапеция КМ=РТ=6 см, МР=5 см, КТ=12 см, ∠К=∠Т=30°. S(КМРТ) - ?
ΔРТН - прямоугольный, ∠Т=30°, значит РН=1/2 РТ = 6:2=3 см.
S=(МР+КТ):2*РН=(5+12):2*3=25,5 см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: olja101283
Предмет: Русский язык,
автор: svl3
Предмет: Английский язык,
автор: KateSkr
Предмет: Французский язык,
автор: KenanAliyev27
Предмет: Математика,
автор: natalliel