Предмет: Геометрия,
автор: bpan93rus
помогите пожалуйста! как найти стороны в треугольнике если известен угол и высота
Приложения:
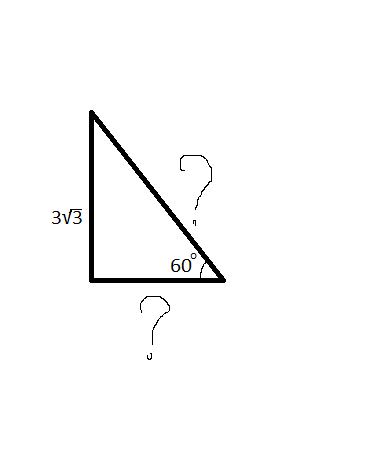
Ответы
Автор ответа:
0
Обозначим меньший катет "а", больший катет "b" (b=3*√(3)), гипотенузу "с".
Если уже знаешь тригонометрию, то так: a=b/tg(60°)=3*√(3)/√(3)=3,
или a=b*ctg(60°)=3*√(3)/(√(3)/3)=3.
c=b/sin(60°)=3*√(3)/(√(3)/2)=6.
Если еще не знаешь тригонометрию, то так:
Сумма острых углов в прямоугольном треугольнике равна 90°. Если один равен 60°, то другой равен 30°. А у прямоугольного треугольника с с острым углом в 30° есть такое свойство: "катет, лежащий против угла в 30°, равен половине гипотенузы". Пусть меньший катет (лежащий против угла в 30°) равен "х". Тогда гипотенуза равна 2*х, а больший катет по теореме Пифагора
.равен √((2*х)^2-(^2))=х*√(3). Таким образом, нужно запомнить, что в прямоугольном треугольнике с острым углом в 30° стороны относятся как 1:√(3):2. А теперь осталось составить и решить пропорции. a:b:c=1:√(3):2. Отсюда с=6, а=3.
Если уже знаешь тригонометрию, то так: a=b/tg(60°)=3*√(3)/√(3)=3,
или a=b*ctg(60°)=3*√(3)/(√(3)/3)=3.
c=b/sin(60°)=3*√(3)/(√(3)/2)=6.
Если еще не знаешь тригонометрию, то так:
Сумма острых углов в прямоугольном треугольнике равна 90°. Если один равен 60°, то другой равен 30°. А у прямоугольного треугольника с с острым углом в 30° есть такое свойство: "катет, лежащий против угла в 30°, равен половине гипотенузы". Пусть меньший катет (лежащий против угла в 30°) равен "х". Тогда гипотенуза равна 2*х, а больший катет по теореме Пифагора
.равен √((2*х)^2-(^2))=х*√(3). Таким образом, нужно запомнить, что в прямоугольном треугольнике с острым углом в 30° стороны относятся как 1:√(3):2. А теперь осталось составить и решить пропорции. a:b:c=1:√(3):2. Отсюда с=6, а=3.
Автор ответа:
0
спасибо большое!))
Похожие вопросы
Предмет: Русский язык,
автор: matveybulushev77
Предмет: Математика,
автор: esskeetit1mans
Предмет: Математика,
автор: olga8552
Предмет: Математика,
автор: djkristi
Предмет: Математика,
автор: sobaka857365786