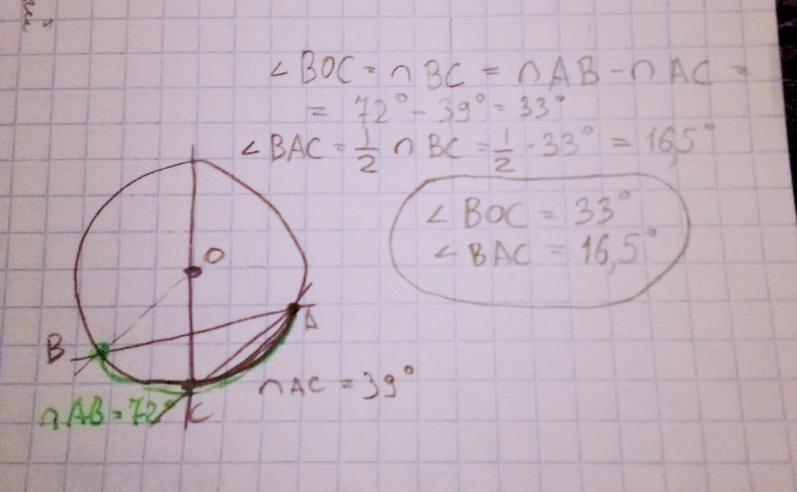ПОМОГИТЕ Пожалуйста. !!!!!!!!!!
Два угла четырехугольника равны 110° и 120°. Найдите оставшиеся углы четырехугольника, если его можно вписать в окружность. 70° и 60° 80° и 50° 72° и 58° 65° и 65° Вопрос №2 ? 2 балла Градусная мера дуги АВ равна 72о, а дуги АС – 39о, при этом точки А и В лежат в разных полуплоскостях относительно диаметра окружности, проходящего через точку С. Найдите углы ВОС и ВАС, где О – центр окружности 111о и 55,5о 66о и 33о 33о и 16,5о 144о и 78о Вопрос №3 ? 2 балла Точки А и В лежат по одну сторону от прямой на расстоянии 2 см и 10 см от нее. Найдите расстояние от точки М до прямой, если М лежит между А и В и АМ : МВ = 1 : 3. 4 5 6 3 Вопрос №4 ? 2 балла На рисунке ABCD – описанная трапеция, точка О – центр окружности. Найдите РABCD. Ответ Вопрос №5 ? 2 балла В четырехугольнике ABCD AB=10 см, BC=8 см, CD=7 см. Какой длины должна быть сторона AD, чтобы этот четырехугольник можно было описать около окружности? Ответ Вопрос №6 ? 2 балла Найдите среднюю линию трапеции, описанной около окружности, если ее боковые стороны равны 5 см и 7 см. Ответ
Ответы
Ответ:
№1
Объяснение:
Если четырёхугольник можно вписать в окружность, значит в этом четырёхугольнике сумма противолежащих углов равна 180° ⇒
⇒ угол, лежащий против угла в 120° равен 180° - 120° = 60° и угол, лежащий против угла в 150°, равен 180° - 150° = 30°
Так как вершины четырёхугольника лежат на окружности, его углы будут являться вписанными и отсюда, градусные меры дуг, на которые эти углы опираются, будут в два раза больше самих углов.
Находим, что углы в 60° и 30° четырёхугольника опираются на дуги в 120° и 60°
№2 (фото)
№3 Ответ:4
№4ОЕ⊥СD⇒ ОЕ - радиус.
АВ⊥ВС и АD
Проведем OK⊥АВ
ОК=r
OH⊥AD
АН=ОК=OE=6
HD=ED=9
AD=AH+HD=15
Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.
Трапеция - четырехугольник.
ВС+AD=AB+CD
Р=ВС+AD+AB+CD=2•(10+15)=50 см
——————————————————
4. На рис. 134 точка О – центр вписанной окружности, угол А=углу С, BD=18 см, BO:OD=5:4. Найдите стороны треугольника.
DO+ВО=9х ⇒
х=18:9=2
OD=8, ВО=10.
По условию углы при АС равны. ⇒ ∆ АВС - равнобедренный, АВ=ВС.
Центр вписанной в треугольник окружности лежит на биссектрисе.
Биссектриса равнобедренного треугольника - высота и медиана. ⇒
∠BDA=90°
AD=CD.
Проведем ОН - перпендикуляр в точку касания на АВ.
Из ∆ ВОН по т.Пифагора ВН=6
В прямоугольных ∆ АВD и ∆ OBH острый угол при В общий.⇒
∆ АВD~∆ OBH
Из подобия следует отношение
АВ:ВО=ВD:BH
AB•6=10•18⇒
AB=180:6=30
По т.Пифагора AD=24 ⇒
АС=48
ВС=АD=30
№5В чотирикутник можна вписати коло тоді й тільки тоді, коли суми його протилежних сторін рівні.
Таким чином,
AB+CD= BC+AD;
10+7= 8+AD;
17=8+AD;
AD= 17-8;
AD= 9.
Відповідь: якщо AD=9 см, то в даний чотирикутник можна вписати коло.
№6если трапеция описана около окружности, то сумма оснований равна сумме боковых сторон, а средняя линия равна полусумме оснований,тогда средняя линия = (5+7)/2=6