Предмет: Геометрия,
автор: dum1313hdrhb
найдите пожалуйста стороны
Приложения:
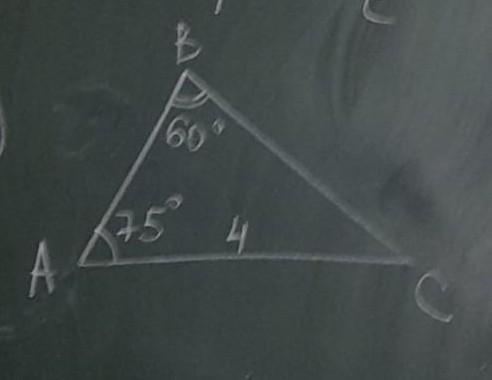
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: ева280
Предмет: Русский язык,
автор: Sanya171
Предмет: Математика,
автор: krivoruchkay