Предмет: Алгебра,
автор: KaktusiVerblud
Помогите, пожалуйста, решить уравнение. Алгебра 9 класс
Заранее спасибо
Приложения:
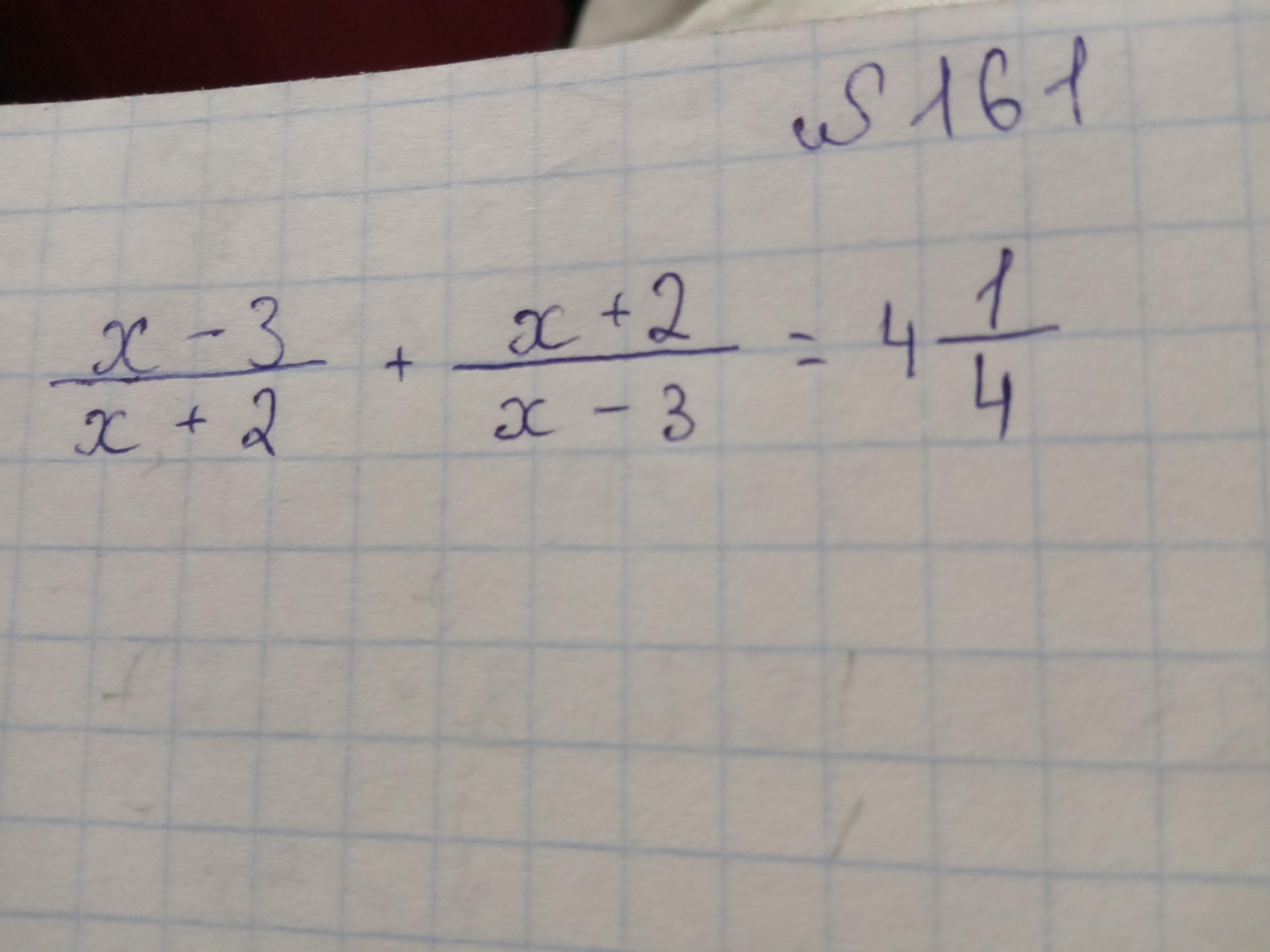
Ответы
Автор ответа:
2
2 ответа x=14/3 и x=-11/3
4t²+4-17t=0
4t²-17t+4=0
вычисляем дискриминант:
D=(-17)²=289-64=225
x(1)=17-15/8=1/4
x(2)=17+15 /8 =32:8=4
Приложения:

Автор ответа:
2
ОДЗ: х≠-2; х≠3;
Пусть t=[(x-3)]/[(x+2)].
ОДЗ: t≠0.
D=(-17)²-4*4*4=289-64=225=15²
Обратная замена: t=[(x-3)]/[(x+2)].
Ответ: -11/3 и 14/3.
Похожие вопросы
Предмет: Русский язык,
автор: danilaaprel100
Предмет: Русский язык,
автор: ксения739
Предмет: Другие предметы,
автор: ostrik
Предмет: Математика,
автор: rore24
Предмет: Алгебра,
автор: isagaliev28