Предмет: Алгебра,
автор: dum1389
срочно нужно найти треугольник дам 85б
Приложения:
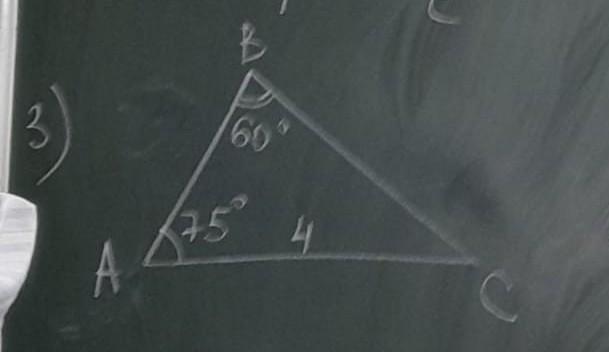
casesgo364:
Ну так вот він що ще треба?
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Окружающий мир,
автор: madamsherbakova
Предмет: Қазақ тiлi,
автор: бота29
Предмет: Английский язык,
автор: olegmuzykin19
Предмет: Математика,
автор: Аноним
Предмет: Қазақ тiлi,
автор: Azara76