Question

помогите пожалуйста решить
Дана треугольная пирамида ABCD
Найти угол между прямыми АD и BC, если AD=24, BC=10, а расстояние между серединами ребер BD и AC равно 13

Answer 1

Ответ:

∠FGE=90°.

Пошаговое объяснение:

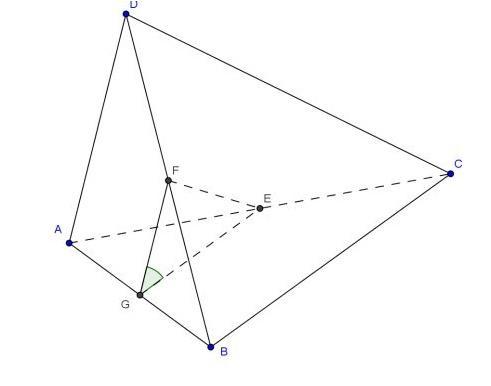
Пусть Е - середина ребра АС, F- середина ребра BD, EF=13.

Прямые АD и ВС - скрещивающиеся, а угол между скрещивающимися прямыми равен углу между параллельными им прямыми, проходящими через одну точку. Проведем через точку Е прямую EG||BC и пусть G - точка пересечения этой прямой со стороной АВ. Очевидно, что G - середина АВ. Соединим G с F так как G и F -середины АВ и ВD соответственно, то GF - средняя линия треугольника АВD, а значит, GF||AD. Таким образом, угол между прямыми AD и ВС равен углу между GF и GE, то есть углу FGE.

Учитывая, что GF и GE - средние линии, имеем GF=12, GE=5, откуда по теореме, обратной теореме Пифагора, ∠FGE=90°.