Предмет: Алгебра,
автор: va7ili4
Нужна помощь с 13 срочно
Приложения:
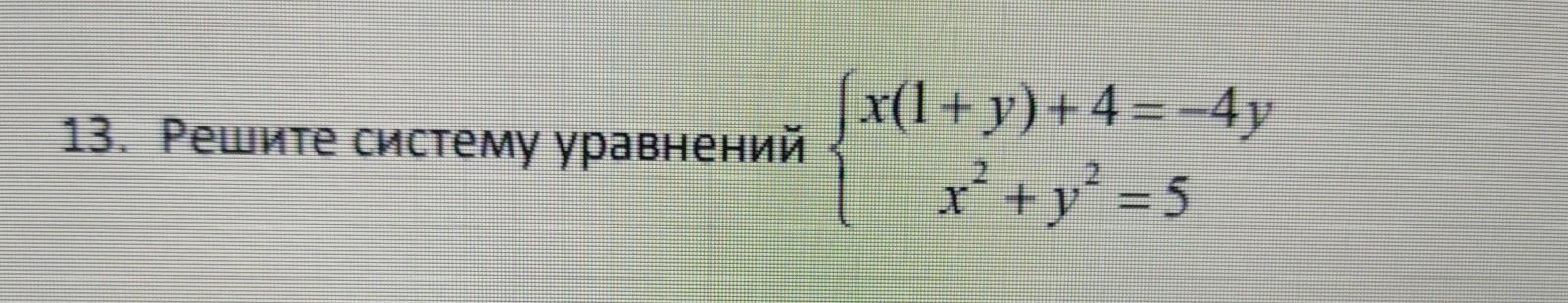
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
2
Похожие вопросы
Предмет: Окружающий мир,
автор: mirzaga55
Предмет: Қазақ тiлi,
автор: салта17
Предмет: Русский язык,
автор: Аноним
Предмет: Литература,
автор: vladakovalenko
Предмет: История,
автор: karina20072007