Question

Помогите пожалуйста срочно!!!!!!
Обчисліть площу фігури обмеженою параболою

$y = x {}^{2} + 4x + 4$
та прямою
$y = x + 4$


​​

Answer 1

Ответ:

9/2

Пошаговое объяснение:

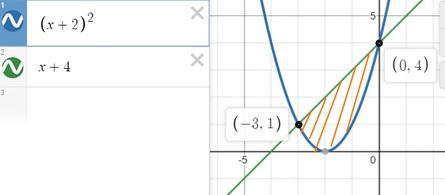
Чертим графики, получаем область фигуры и затем по формуле Ньютона-Лейбница вычисляем площадь.

Формула Ньютона-Лейбница

$\displaystyle S=\int\limits^a_b {\bigg (y_1(x)-y_2(x)\bigg )} \, dx$

Первый график

$y=x^2+4x+4\\\\x^2+4x+4 = (x+2)^2$

Значит мы берем известный график функции у=х² и смещаем его по оси ОХ на (-2)/

Второй график строим по двум точкам

х    0    1

у    4    5

Графики построили, получили пределы интегрирования

а = -3;  b = 0

За у₁(х) принимаем функцию, график которой находится "выше" на интервале [a^ b].

У нас это функция

у₁(х) = х + 4

Теперь находим площадь

$\displaystyle S=\int\limits^0_{-3} \bigg ({(x+4)-(x^2+4x+4)\bigg )} \, dx =\\\\=\int\limits^0_{-3} {(-x^2-3x)} \, dx =-\frac{x^3}{3} \bigg |_{-3}^0-\frac{3x^2}{2} \bigg |_{-3}^0=-9+\frac{27}{2} =\frac{9}{2}$

ответ

S = 9/2