Предмет: Алгебра,
автор: zakazagona20
Решите дробно-рациональное уравнение
Приложения:
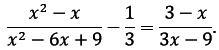
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: паша0306
Предмет: Қазақ тiлi,
автор: айдос80
Предмет: Английский язык,
автор: kotiwow
Предмет: Русский язык,
автор: dragasiyeva