Question

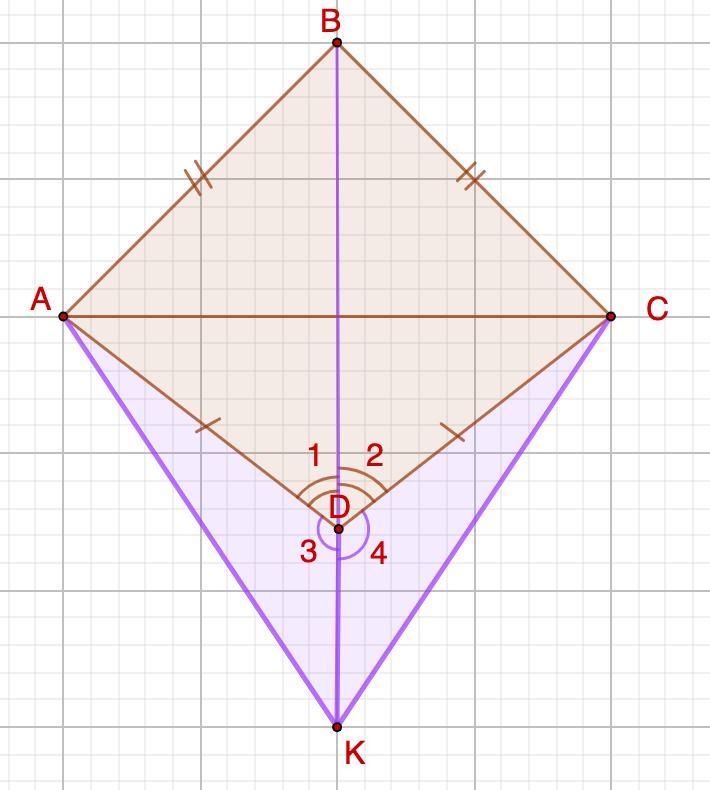
Вершины B и D треугольников ABC и ADC лежат в разных полуплоскостях относительно прямой АС, АВ = ВС, AD = DC. Точка К лежит на луче BD так, что точка D лежит между точками B и K. Докажите, что треугольники ADK и СDK равны.

Answer 1

Ответ:

Объяснение:

Дано: ΔABC и ΔABD.

АВ = ВС, AD = DC.

Доказать:

ΔADK = ΔСDK

Доказательство:

1. Рассмотрим ΔABD и ΔDBC.

АВ = ВС, AD = DC (по условию)

DB - общая.

⇒ ΔABD = ΔDBC (по трем сторонам, 3 признак)

• В равных треугольниках против равных сторон лежат равные углы.

⇒ ∠1 = ∠2.

2. Рассмотрим ΔADK и ΔСDK.

AD = DC (по условию);

DК - общая.

• Сумма смежных углов равна 180°.

⇒ ∠3 = 180° - ∠1 (смежные)

    ∠4 = 180° - ∠2 (смежные)

Так как ∠1 = ∠2 (п.1) ⇒ ∠3 = ∠4

⇒ ΔADK = ΔСDK (по двум сторонам и углу между ними, 1 признак)