Предмет: Алгебра,
автор: villiwonkka1
N•16
P.s полностью
_._._._._._ ._._._
Приложения:
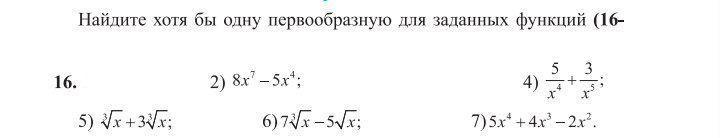
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Приложения:
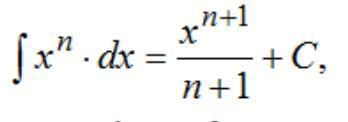
villiwonkka1:
Проентегрируйте пожалуйста
а потом ответ
ввиде интегралов
Похожие вопросы
Предмет: Қазақ тiлi,
автор: 12345Дияс
Предмет: Русский язык,
автор: vanyshakiselev
Предмет: Русский язык,
автор: kelmesku333
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: SashaSakha