Предмет: Алгебра,
автор: ngnfcng
45б. За формулою Ньютона-Лейбніца, обчислити інтеграл. Детально розписати
Приложения:
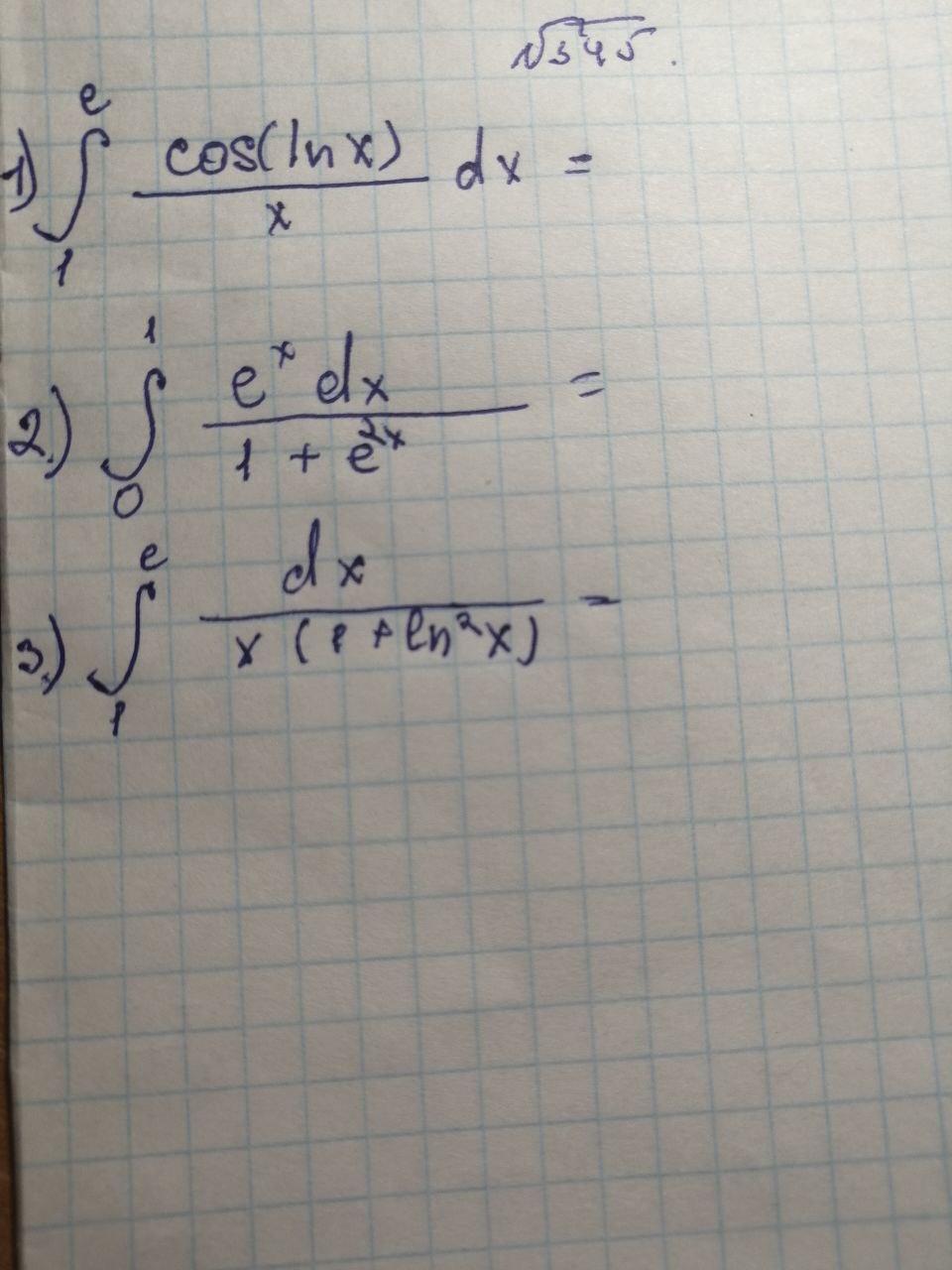
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: ruslan1071
Предмет: Русский язык,
автор: Lino1998
Предмет: Русский язык,
автор: ОляЯ11
Предмет: Русский язык,
автор: drhkxxgjlxgjjfpx
Предмет: Английский язык,
автор: AlExAnDeR600