Question

Kаковы должны быть размеры открытого цилиндрического бака объёмом 128π, чтобы на его изготовление ушло наименьшее количество материала?

Answer 1

Ответ:

R≅5,04

H≅5,04

Объяснение:

Объём цилиндра :

(1)  V = πR²H,

где R - радиус цилиндра, H - высота цилиндра.

Площадь полной поверхности цилиндра:

(2) S = πR² + 2πRH

Выразим из формулы (1) высоту цилиндра и подставим значение в формулу (2):

$H= \dfrac{V}{\pi R^{2} } =\dfrac{128\pi }{\pi R^{2} } =\dfrac{128}{R^{2} } \\\\S = \pi R^{2} +2\pi R\dfrac{128}{R^{2} } = \pi R^{2} + \dfrac{256\pi }{R}$

Найдём минимум этой функции по переменной R. Для этого вычислим производную и определим критические точки.

$S' = (\pi R^{2} +\dfrac{256\pi }{R} )' = 2\pi R-256\pi \dfrac{1}{R^{2} }$.

S' = 0,

$\dfrac{2\pi R^3-256\pi }{R^{2} } = 0$

Если R = 0, то производная не существует.

$2\pi (R^3-128)=0\\\\R^3 = 128\\\\R=\sqrt[3]{128}$

R≅ 5.04

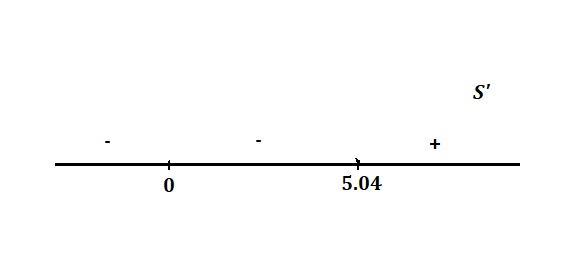
Отметим эти значения на координатной прямой и oпределим знак производной на трёх полученных числовых интервалах. (Cм.рис)

Известно, что в точке минимумa производная меняет знак с минусa на плюс. Соответственно,  наименьшее количество материала можно получить, если радиус основания цилиндра R=5,04

Вычислим соответствующую высоту цилиндра:

$H = \dfrac{128}{R^{2} } =\dfrac{128}{5,04^{2} } =\dfrac{128}{25,40} = 5,04$