постройте график функции
у= х³-2х²/(х-2)
по плану:
написать область определения функции
во что превращается функция после упрощения
ответ на вопрос: при каком значении а прямая у=а имеет с графиком ровно 2 общих точки ?
у||х, у=а
Ответы
Ответ:
В решении.
Объяснение:
Постройте график функции
у= х³-2х²/(х-2)
по плану:
1) Во что превращается функция после упрощения?
у = (х²(х - 2))/(х - 2);
Сократить числитель и знаменатель на (х - 2), функция превращается в уравнение квадратичной функции у = х².
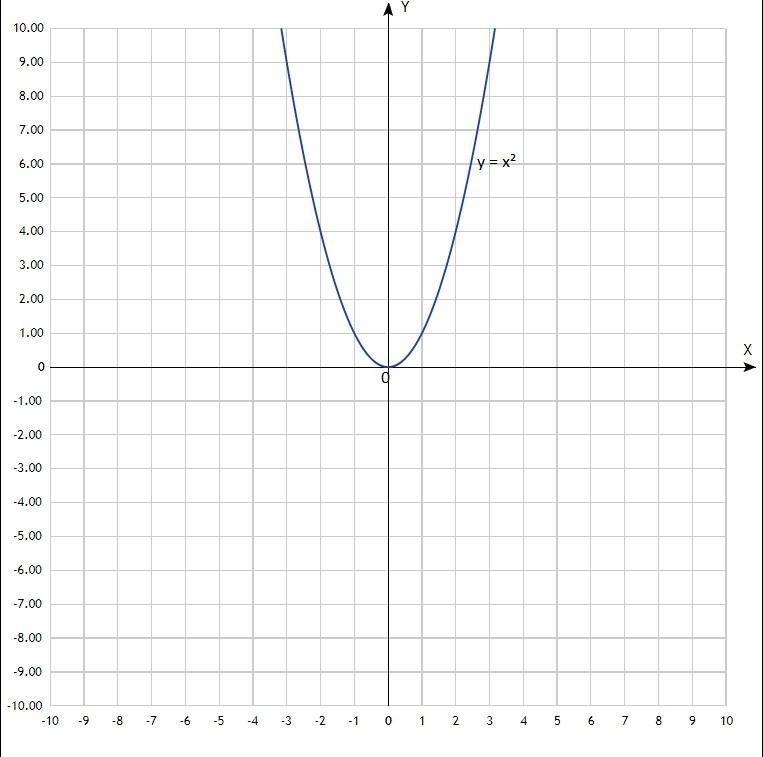
График - парабола с центром в начале координат (0; 0), ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3
у 9 4 1 0 1 - 9
2) Написать область определения функции.
Область определения - это проекция графика функции на ось Ох.
Обозначается как D(f) или D(у).
Область определения параболы - множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.
Обычно запись: D(у) = R.
Но, так как х в знаменателе, по ОДЗ х не может быть равен 2, поэтому область определения данной функции - множество всех действительных чисел, кроме х = 2. В этой точке функция не определена.
D(у) = R : х ≠ 2.
3) Ответ на вопрос: при каком значении а прямая у=а имеет с графиком ровно 2 общих точки ?
Согласно графика, при любом а > 0 (весь график выше оси Ох).