Question

пж помогите с контрольной она у меня завтра!!!!​ УМОЛЯЮ

Answer 1

Объяснение:

1.

$f(x)=3x^2-2x\\1)\ f(-6)=3*(-6)^2-2*(-6)=3*36+12=108+12=120.\\f(2)=3*2^2-2*2=3*4-4=12-4=8.\\2)\ x=0\ \ \ \ \ y=3*0^2-2*0\ \ \ \ y=0\ \ \ \ \ \Rightarrow\ \ \ \ (0;0).\\3x^2-2x=0\\x*(3x-2)=0\\x_1=0\ \ \ \ y_1=0.\\3x-2=0\\x=\frac{2}{3}.\ \ \ \ \ \ y=3*(\frac{2}{3})^2-2*\frac{2}{3} =\frac{3*4}{3^2} -\frac{4}{3}=\frac{4}{3}-\frac{4}{3}=0\ \ \ \ \ y=0\ \ \ \ \Rightarrow\ \ \ \ (\frac{2}{3};0).$

Ответ: (0;0),  (2/3;0).

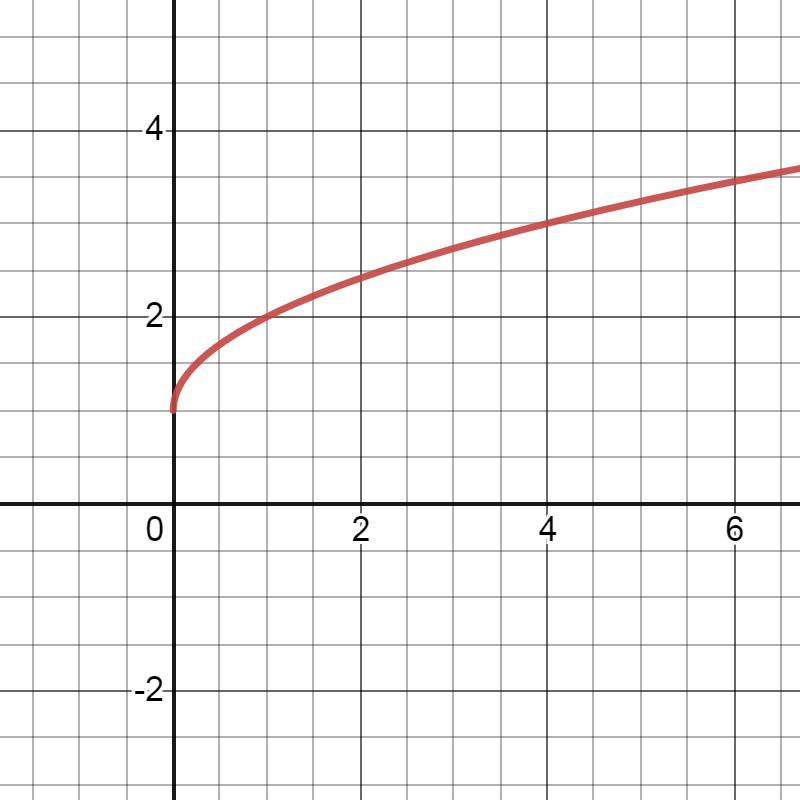
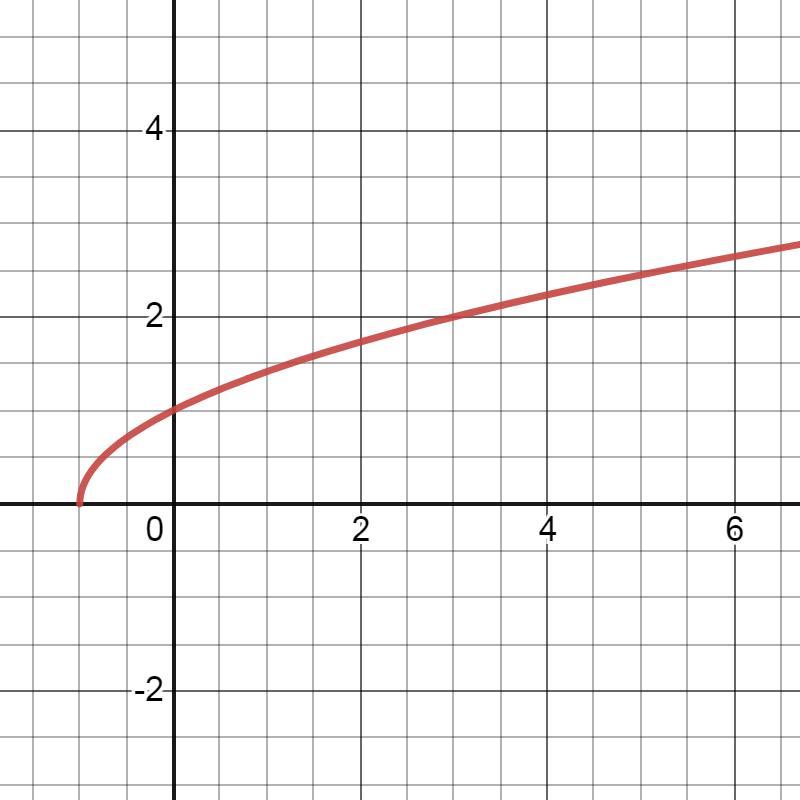
2.

$y=x^2-4x+3=x^2-2*x*2+4-4+3=x^2-4x+2^2-1=(x-2)^2-1.$

Это график функции у=х², смещённый вправо вдоль оси ОХ

на 2 единицы и опущенный вниз вдоль оси ОУ на 1 единицу.

1) область значения функции:

$y=(x-2)^2-1\\(x-2)^2=y+1\\x-2=\sqrt{y+1}\\x=\sqrt{y+1}+2\\y+1\geq 0\\y\geq -1 . \ \ \ \ \ \Rightarrow\\y\in[-1;+\infty).$

2) промежуток убывания функции: x∈(-∞;2).

3) значения х, при которых y>0: x∈(-∞;1)U(3;+∞).

3.

$1)\ y=\sqrt{x} +1.\\2)\ y=\sqrt{x+1}.$

4.

$y=\frac{x-4}{x^2-x-6} \\x^2-x-6\neq 0\\x^2-3x+2x-6\neq 0\\x*(x-3)+2*(x-3)\neq =\\(x-3)*(x+2)\neq 0\\x-3\neq 0\\x\neq 3.\\x+2\neq 0\\x\neq -2.\ \ \ \ \ \Rightarrow\\x\in(-\infty;-2)U(3;+\infty).$

5.

$x^2-3x-1=-\frac{3}{x} \\y=x^2-3x-1. \ \ \ \ \ \ \ y=-\frac{3}{x} .$

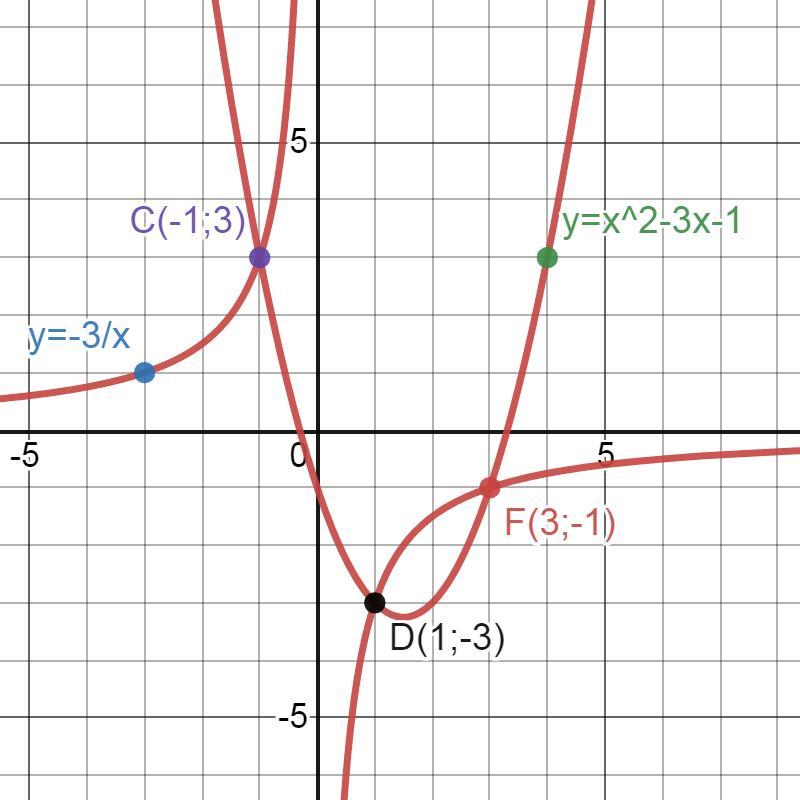
Ответ: (-1;3),  (1;-3),  (3;-1).