Предмет: Геометрия,
автор: lli82
СРОЧНО ДАЮ 50 БАЛЛОВ
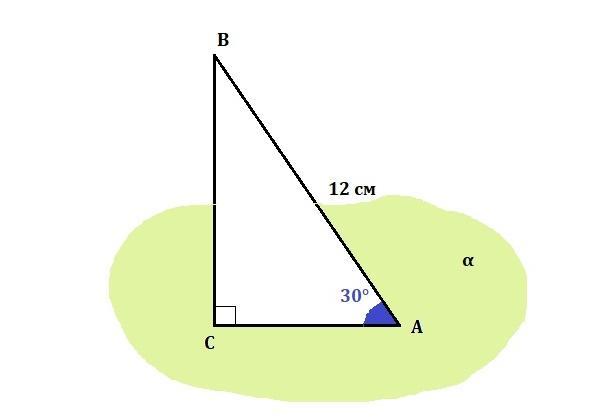
К плоскости α проведена наклонная AB (A∈α). Длина наклонной равна 12 см, наклонная с плоскостью образует угол 30°. Вычисли, на каком расстоянии от плоскости находится точка B.
Расстояние от точки B до плоскости равно ____√____ см.
(Если в ответе нет корня, то под корнем пиши 1.)
Ответы
Автор ответа:
2
Ответ:
6√1 см.
Объяснение:
АВ - наклонная. АВ = 12 см
- Наклонной, проведённой из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.
Проведём из вершины В перпендикуляр ВС на плоскость α
ВС⊥α
- Перпендикуляром, проведённым из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости, и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
- Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых из одной и той же точки, называется проекцией наклонной.
АС - проекция наклонной АВ. ΔАВС - прямоугольный (∠С=90°)
- Угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость.
Угол ВАС - это угол между наклонной АВ и плоскостью α. ∠ВАС = 30° - по условию
- Расстояние от точки до плоскости — равно длине перпендикуляра ВС, опущенного из точки на плоскость α
- В прямоугольном треугольнике катет, лежащий против угла в 30° равен половине гипотенузы.
Расстояние от точки B до плоскости равно 6√1 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: SvetaBelka
Предмет: Қазақ тiлi,
автор: sabina156
Предмет: Другие предметы,
автор: madya666
Предмет: Математика,
автор: kostys1061
Предмет: История,
автор: Snejoklol